※数据结构※→☆非线性构造（tree）☆============哈夫曼树 链式存储结构（tree Huffman list）（二十三）

※数据结构※→☆非线性结构（tree）☆============哈夫曼树 链式存储结构（tree Huffman list）（二十三）

哈夫曼树 (Huffman Tree)
        给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)。

哈夫曼树（霍夫曼树）又称为最优树.
        1、路径和路径长度
                在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。
        2、结点的权及带权路径长度
                若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。
        3、树的带权路径长度
                树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

哈夫曼树构造过程
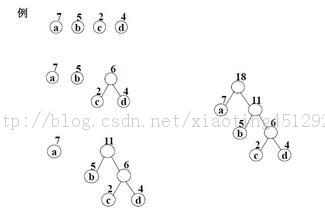
        假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；(3)从森林中删除选取的两棵树，并将新树加入森林；(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。        
         构造过程中，需要使用优先级队列，由于优先级队列存储的仅仅只是指针，因此需要使用伪函数(操作符operator () )自定义排序。
函数对象（伪函数）
         实现了一个"()"操作符，这样就允许把这个类像函数一样使用，我们把这样的类称为函数对象，或称做伪函数。可以把实例当作一个函数来使用。
         优点：使用仿函数就像使用一个普通的函数一样，但是它的实现可以访问仿函数中所有的成员变量来进行通行；而普通函数若要通信就只能依靠全局变量了。

         函数对象顾名思义，就是在某种方式上表现的象一个函数的对象。典型的，它是指一个类的实例，这个类定义了应用操作符operator()。
         函数对象是比函数更加通用的概念，因为函数对象可以定义跨越多次调用的可持久的部分（类似静态局部变量），同时又能从对象的外面进行初始化和检查（和静态局部变量不同）

树的四种遍历
        1.先序遍历 （仅二叉树）
                指先访问根，然后访问孩子的遍历方式

        2.中序遍历（仅二叉树）
                指先访问左（右）孩子，然后访问根，最后访问右（左）孩子的遍历方式

        3.后序遍历（仅二叉树）
                指先访问孩子，然后访问根的遍历方式

        4.层次遍历
                一层一层的访问，所以一般用广度优先遍历。

======================================================================================================
树结点 链式存储结构（tree node list）
结点：
        包括一个数据元素及若干个指向其它子树的分支；例如，A，B，C，D等。
在数据结构的图形表示中，对于数据集合中的每一个数据元素用中间标有元素值的方框表示，一般称之为数据结点，简称结点。

        在C语言中，链表中每一个元素称为“结点”，每个结点都应包括两个部分：一为用户需要用的实际数据；二为下一个结点的地址，即指针域和数据域。

        数据结构中的每一个数据结点对应于一个储存单元，这种储存单元称为储存结点，也可简称结点

树结点（树节点）：
        

树节点相关术语：
节点的度：一个节点含有的子树的个数称为该节点的度；叶节点或终端节点：度为0的节点称为叶节点；非终端节点或分支节点：度不为0的节点；双亲节点或父节点：若一个结点含有子节点，则这个节点称为其子节点的父节点；孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；兄弟节点：具有相同父节点的节点互称为兄弟节点；节点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；堂兄弟节点：双亲在同一层的节点互为堂兄弟；节点的祖先：从根到该节点所经分支上的所有节点；子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
        根据树结点的相关定义，采用“双亲孩子表示法”。其属性如下：


        2．孩子表示法
                1.多重链表：每个结点有多个指针域，分别指向其子树的根
                        1）结点同构：结点的指针个数相等，为树的度k,这样n个结点度为k的树必有n(k-1)+1个空链域.
                                                
                        2）结点不同构：结点指针个数不等，为该结点的度d
                                                

                2.孩子链表：每个结点的孩子结点用单链表存储，再用含n个元素的结构数组指向每个孩子链表
                

        3．双亲孩子表示法
                1.双亲表示法，PARENT（T，x）可以在常量时间内完成，但是求结点的孩子时需要遍历整个结构。
                2.孩子链表表示法，适于那些涉及孩子的操作，却不适于PARENT（T，x）操作。
                3.将双亲表示法和孩子链表表示法合在一起，可以发挥以上两种存储结构的优势，称为带双亲的孩子链表表示法
                

        4．双亲孩子兄弟表示法 （二叉树专用）
                又称为二叉树表示法，以二叉链表作为树的存储结构。
                                
                

链式存储结构
        在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的).
        它不要求逻辑上相邻的元素在物理位置上也相邻.因此它没有顺序存储结构所具有的弱点,但也同时失去了顺序表可随机存取的优点.


        链式存储结构特点：
                1、比顺序存储结构的存储密度小 (每个节点都由数据域和指针域组成，所以相同空间内假设全存满的话顺序比链式存储更多)。
                2、逻辑上相邻的节点物理上不必相邻。
                3、插入、删除灵活 (不必移动节点，只要改变节点中的指针)。
                4、查找结点时链式存储要比顺序存储慢。
                5、每个结点是由数据域和指针域组成。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
以后的笔记潇汀会尽量详细讲解一些相关知识的，希望大家继续关注我的博客。
本节笔记到这里就结束了。


潇汀一有时间就会把自己的学习心得，觉得比较好的知识点写出来和大家一起分享。
编程开发的路很长很长，非常希望能和大家一起交流，共同学习，共同进步。
如果文章中有什么疏漏的地方，也请大家指正。也希望大家可以多留言来和我探讨编程相关的问题。
最后，谢谢你们一直的支持~~~


       C++完整个代码示例（代码在VS2005下测试可运行）
       

AL_TreeNodeBinList.h
#ifdef TEST_AL_TREEHUFFMANLISTAL_TreeHuffmanList<DWORD> cTreeHuffman;BOOL bEmpty = cTreeHuffman.IsEmpty();std::cout<<bEmpty<<std::endl;const AL_TreeNodeBinList<DWORD>* pConstRootNode = cTreeHuffman.GetRootNode();AL_TreeNodeBinList<DWORD>* pRootNode = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstRootNode);std::cout<<pRootNode<<std::endl;DWORD dwDegree = cTreeHuffman.GetDegree();std::cout<<dwDegree<<std::endl;DWORD dwHeight = cTreeHuffman.GetHeight();std::cout<<dwHeight<<std::endl;DWORD dwNodesNum = cTreeHuffman.GetNodesNum();std::cout<<dwNodesNum<<std::endl;DWORD dwWeight = 0x01;cTreeHuffman.InsertRoot(0, dwWeight);pConstRootNode = cTreeHuffman.GetRootNode();pRootNode = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstRootNode);std::cout<<pRootNode<<std::endl;dwWeight += 2;cTreeHuffman.InsertLeftAtNode(pRootNode, 10, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode = cTreeHuffman.GetChildNodeLeftAtNode(pRootNode);AL_TreeNodeBinList<DWORD>* pTreeNode = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode);std::cout<<pTreeNode<<std::endl;dwWeight += 2;cTreeHuffman.InsertLeftAtNode(pTreeNode, 20, dwWeight);dwWeight += 2;cTreeHuffman.InsertRightAtNode(pTreeNode, 21, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode20 = cTreeHuffman.GetChildNodeLeftAtNode(pTreeNode);AL_TreeNodeBinList<DWORD>* pTreeNode20 = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode20);std::cout<<pTreeNode<<std::endl;dwWeight += 2;cTreeHuffman.InsertLeftAtNode(pTreeNode20, 30, dwWeight);dwWeight += 2;cTreeHuffman.InsertRightAtNode(pTreeNode20, 31, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode31 = cTreeHuffman.GetChildNodeRightAtNode(pConstTreeNode20);AL_TreeNodeBinList<DWORD>* pTreeNode31 = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode31);dwWeight += 2;cTreeHuffman.InsertLeftAtNode(pTreeNode31, 40, dwWeight);dwWeight += 2;cTreeHuffman.InsertRightAtNode(pTreeNode31, 41, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode30 = cTreeHuffman.GetChildNodeLeftAtNode(pConstTreeNode20);AL_TreeNodeBinList<DWORD>* pTreeNode30 = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode30);dwWeight += 2;cTreeHuffman.InsertRightAtNode(pTreeNode30, 999, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode999 = cTreeHuffman.GetChildNodeRightAtNode(pConstTreeNode30);AL_TreeNodeBinList<DWORD>* pTreeNode999 = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode999);dwWeight += 2;cTreeHuffman.InsertLeftAtNode(pTreeNode999, 888, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode41 = cTreeHuffman.GetChildNodeRightAtNode(pConstTreeNode31);AL_TreeNodeBinList<DWORD>* pTreeNode41 = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode41);dwWeight += 2;cTreeHuffman.InsertRightAtNode(pTreeNode41, 52, dwWeight);const AL_TreeNodeBinList<DWORD>* pConstTreeNode33 = cTreeHuffman.GetChildNodeRightAtNode(pTreeNode20);AL_TreeNodeBinList<DWORD>* pTreeNode33 = const_cast<AL_TreeNodeBinList<DWORD>*>(pConstTreeNode33);if (NULL != pTreeNode) {std::cout<<pTreeNode->GetLevel()<<"    "<<pTreeNode->GetData()<<"    "<<pTreeNode->GetDegree()<<std::endl;std::cout<<pTreeNode->IsLeaf()<<"    "<<pTreeNode->IsBranch()<<"    "<<pTreeNode->IsParent(pTreeNode)<<"    "<<pTreeNode->IsParent(pTreeNode33)<<std::endl;}if (NULL != pTreeNode20) {std::cout<<pTreeNode20->GetLevel()<<"    "<<pTreeNode20->GetData()<<"    "<<pTreeNode20->GetDegree()<<std::endl;std::cout<<pTreeNode20->IsLeaf()<<"    "<<pTreeNode20->IsBranch()<<"    "<<pTreeNode20->IsParent(pTreeNode)<<"    "<<pTreeNode20->IsParent(pTreeNode33)<<std::endl;}if (NULL != pTreeNode33) {std::cout<<pTreeNode33->GetLevel()<<"    "<<pTreeNode33->GetData()<<"    "<<pTreeNode33->GetDegree()<<std::endl;std::cout<<pTreeNode33->IsLeaf()<<"    "<<pTreeNode33->IsBranch()<<"    "<<pTreeNode33->IsParent(pTreeNode)<<"    "<<pTreeNode33->IsParent(pTreeNode33)<<std::endl;}const AL_TreeNodeBinList<DWORD>*pChild = NULL;pChild = cTreeHuffman.GetChildNodeRightAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<"    "<<pChild->GetData()<<"    "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<"    "<<pChild->IsBranch()<<"    "<<pChild->IsParent(pTreeNode)<<"    "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeHuffman.GetChildNodeLeftAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<"    "<<pChild->GetData()<<"    "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<"    "<<pChild->IsBranch()<<"    "<<pChild->IsParent(pTreeNode)<<"    "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeHuffman.GetChildNodeLeftAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<"    "<<pChild->GetData()<<"    "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<"    "<<pChild->IsBranch()<<"    "<<pChild->IsParent(pTreeNode)<<"    "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeHuffman.GetChildNodeRightAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<"    "<<pChild->GetData()<<"    "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<"    "<<pChild->IsBranch()<<"    "<<pChild->IsParent(pTreeNode)<<"    "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeHuffman.GetChildNodeRightAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<"    "<<pChild->GetData()<<"    "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<"    "<<pChild->IsBranch()<<"    "<<pChild->IsParent(pTreeNode)<<"    "<<pChild->IsParent(pTreeNode33)<<std::endl;}bEmpty = cTreeHuffman.IsEmpty();std::cout<<bEmpty<<std::endl;dwDegree = cTreeHuffman.GetDegree();std::cout<<dwDegree<<std::endl;dwHeight = cTreeHuffman.GetHeight();std::cout<<dwHeight<<std::endl;dwNodesNum = cTreeHuffman.GetNodesNum();std::cout<<dwNodesNum<<std::endl;AL_ListSingle<DWORD> cList;DWORD dwData;BOOL bSibling = cTreeHuffman.GetSiblingAtNode(pTreeNode, cList);if (TRUE == bSibling) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();bSibling = cTreeHuffman.GetSiblingAtNode(pTreeNode20, cList);if (TRUE == bSibling) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();BOOL bAncestor = cTreeHuffman.GetAncestorAtNode(pRootNode, cList);if (TRUE == bAncestor) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}bAncestor = cTreeHuffman.GetAncestorAtNode(pTreeNode33, cList);if (TRUE == bAncestor) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();BOOL bDescendant = cTreeHuffman.GetDescendantAtNode(pRootNode, cList);if (TRUE == bDescendant) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();bDescendant = cTreeHuffman.GetDescendantAtNode(pTreeNode33, cList);if (TRUE == bDescendant) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();BOOL bOrder = cTreeHuffman.PreOrderTraversal(cList);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();bOrder = cTreeHuffman.InOrderTraversal(cList);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();bOrder = cTreeHuffman.PostOrderTraversal(cList);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();bOrder = cTreeHuffman.LevelOrderTraversal(cList);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cList.Clear();BOOL bConvertToHuffman = cTreeHuffman.ConvertToHuffman();std::cout<<bConvertToHuffman<<std::endl;AL_ListSingle<DWORD> cListWeight;bOrder = cTreeHuffman.LevelOrderTraversal(cList, cListWeight);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData) && TRUE == cListWeight.Get(dwCnt, dwWeight)) {std::cout<<"["<<dwData<<", "<<dwWeight<<"]"<<", ";}}std::cout<<std::endl;}cList.Clear();cListWeight.Clear();dwDegree = cTreeHuffman.GetDegree();std::cout<<dwDegree<<std::endl;dwHeight = cTreeHuffman.GetHeight();std::cout<<dwHeight<<std::endl;dwNodesNum = cTreeHuffman.GetNodesNum();std::cout<<dwNodesNum<<std::endl;cTreeHuffman.RemoveNode(pTreeNode20);bConvertToHuffman = cTreeHuffman.ConvertToHuffman();std::cout<<bConvertToHuffman<<std::endl;bOrder = cTreeHuffman.LevelOrderTraversal(cList, cListWeight);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cList.Length(); dwCnt++) {if (TRUE == cList.Get(dwCnt, dwData) && TRUE == cListWeight.Get(dwCnt, dwWeight)) {std::cout<<"["<<dwData<<", "<<dwWeight<<"]"<<", ";}}std::cout<<std::endl;}bEmpty = cTreeHuffman.IsEmpty();std::cout<<bEmpty<<std::endl;dwDegree = cTreeHuffman.GetDegree();std::cout<<dwDegree<<std::endl;dwHeight = cTreeHuffman.GetHeight();std::cout<<dwHeight<<std::endl;dwNodesNum = cTreeHuffman.GetNodesNum();std::cout<<dwNodesNum<<std::endl;#endif









 

 

查看更多 下一篇