Java基础复习笔记04数据结构-线性表
1.?????? 线性表
线性表是数据结构的一种逻辑结构,其实所有的逻辑数据结构都可以用2类物理实现方式去实现,一个是物理存储连续的顺序结构,另一个就是物理存储不连续的链式结构。线性表是指有n个元素组成的有序序列,这n个元素具有相同的结构。
2.?????? 线性表的操作
线性表的主要操作是增加元素、删除索引处元素、在索引处添加元素、查找索引处元素、替换索引处元素、清空所有元素。而对于顺序结构和链表结构这两种不同实现方式,底层的算法也会有比较大的差异。
3.?????? 使用场景
其实线性表的使用场景非常多,从宏观来说,比如我们从数据库查询多条记录出来需要封装一个集合List对象来承载着众多的业务Bean元素,之后传给MVC的控制C层。之后C层在以某种展现形式传给视图V层。那么装载着众多业务记录信息的容器就是线性表。从微观上来讲,比如实现数据结构的栈结构、或者是对象池的底层、有序排序的数据域等等比较复杂的结构,底层都是离不开线性表的支持。
4.?????? 线性表的顺序实现——顺序表
顺序的存储结构实质上就是利用数组进行元素的存储,笔者简单地实现了一个顺序链表。线性表的顺序实现就是利用对象数组。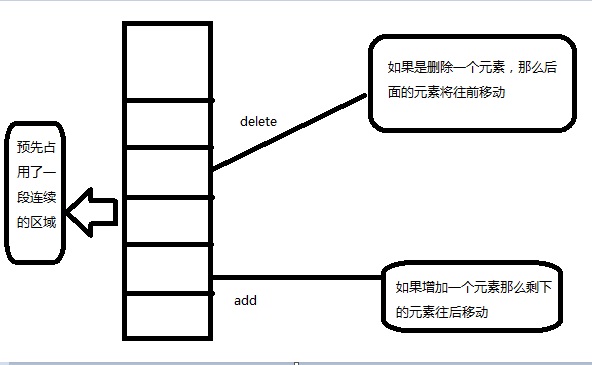
?看如下代码
?
package dateStructer.list;/** * 自实现的arrayList * @author liuyan * * @param <E> */public class MyArrayList<E> implements List<E> {//默认的数组长度private final int DefSize = 16;//临时变量数组private Object[] objects;//记录实实在在的元素个数private int elementSize;public MyArrayList() {objects = new Object[DefSize];}/** * 增加元素,实际上就是往最后一位出入数据 */@Overridepublic boolean add(E e) {add(elementSize, e);return true;}/** * 按位索引插入元素 */@Overridepublic void add(int index, E element) {if (index == elementSize) {objects[index] = element;elementSize++;return;}for (int i = elementSize - 1; i >= 0; i--) {if (i == index) {int movedSize = elementSize - i - 1;System.arraycopy(objects, index + 1, objects, index, movedSize);objects[index] = element;elementSize++;}}}/** * 清除所有元素 */@Overridepublic void clear() {for (int i = 0; i < elementSize; i++) {objects[i] = 0;}elementSize = 0;}/** * 判断集合是否包含了某个元素 */@Overridepublic boolean contains(Object o) {for (Object object : objects) {if (object != null && object.equals(o)) {return true;}}return false;}/** * 获得某位置索引的元素 */@Overridepublic E get(int index) {for (int i = 0; i < elementSize; i++) {if (i == index) {return (E) objects[index];}}return null;}/** * 实现元素定位 */@Overridepublic int indexOf(Object o) {for (int i = 0; i < elementSize; i++) {if (o.equals(objects[i])) {return i;}}return -1;}/** * 是否是空集合 */@Overridepublic boolean isEmpty() {if (elementSize == 0) {return true;}return false;}@Overridepublic int lastIndexOf(Object o) {if (objects == null || objects.length == 0) {return -1;}for (int i = elementSize - 1; i >= 0; i--) {if (objects[i] == o) {return i;}}return -1;}/** * 删除某个元素 */@Overridepublic boolean remove(Object o) {for (int i = 0; i < elementSize; i++) {if (o.equals(objects[i])) {objects[i] = null;int movedSize = elementSize - i - 1;System.arraycopy(objects, i + 1, objects, i, movedSize);elementSize--;return true;}}return false;}/** * 删除某个索引下的元素 */@Overridepublic E remove(int index) {for (int i = 0; i < elementSize; i++) {if (objects[i].equals(objects[index])) {objects[i] = null;int movedSize = elementSize - i - 1;System.arraycopy(objects, i + 1, objects, i, movedSize);elementSize--;return (E) objects[index];}}return null;}/** * 对已有位置设置新的元素值 */@Overridepublic E set(int index, E element) {for (int i = 0; i < elementSize; i++) {if (i == index) {objects[index] = null;objects[index] = element;return element;}}return null;}@Overridepublic int size() {// TODO Auto-generated method stubreturn elementSize;}@Overridepublic String toString() {StringBuffer str = new StringBuffer("[");for (int i = 0; i < elementSize; i++) {str.append("[" + objects[i].toString() + "],");}if (elementSize > 0) {return str.substring(0, str.lastIndexOf(",")) + "]";}return str.append("]").toString();}?实际上实现Java标准的List接口还需要实现其他一些方法,只不过因为篇幅原因,在此只能实现一些核心方法,而且说实在的,根本谈不上健壮性,更不可能投入使用,线程安全也存在问题,这只是演示一下用数组实现顺序线性表的核心算法罢了。所以说学习数据结构实际上是考验算法功底。一个数据结构的事先是否最优,完全是底层算法的实现是否最优。顺序线性表最大的特点就是物理上存储空间连续,内存资源使用比较节省、但是进行增加、删除元素的时候就得让别的元素挪挪地方了,用时间换取了空间的连续性,显得有点牵一发而动全身。如果是查找某个元素操作的时候就是需要遍历整体集合。
简单测试代码如下:
public static void main(String[] args) {MyArrayList<String> list = new MyArrayList<String>();list.add("1");list.add("2");list.add("3");System.out.println(list);list.remove("3");System.out.println(list);list.add("3");System.out.println(list);System.out.println(list.contains("2"));System.out.println(list.isEmpty());list.clear();System.out.println(list);System.out.println(list.isEmpty());}?执行结果
[[1],[2],[3]][[1],[2]][[1],[2],[3]]truefalse[]true
?5.?????? 线性表的非顺序实现——链式表
相对于数组的顺序存储,还可以定义一个比较特殊的链表结构,每个链表节点在内存中不一定是一块连续的区域,链表节点记录了与自身节点相关的下一个节点的位置信息。
如果链表节点仅仅记录了与其下一个Next节点的位置信息,而没有记录上一个Prev节点的信息,那么这叫做单向链表结构。
如果此节点不仅仅记录了下一个节点的信息,还记录了上一个节点的信息,那么这个情况叫做双向链表结构。我们就用双向链表实现Java标准的List<E>接口。(实际上Java提出了一堆标准,实际上就是接口,而sun自己为自己定义的标准接口还提供了实现类,咱们一般用的就是基于sun提出标准的sun自己的实现类)。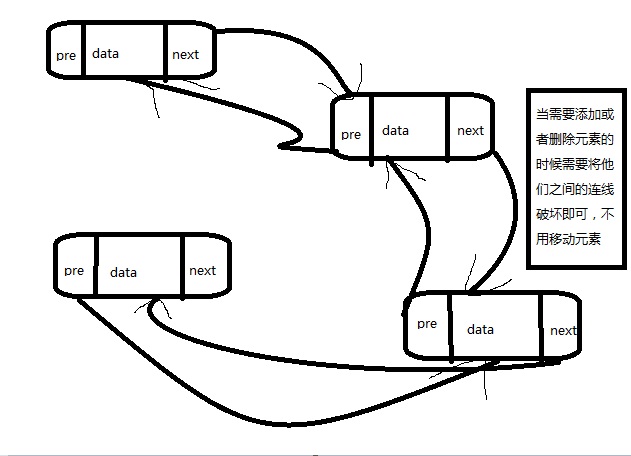
?如下代码
/** * 自己实现的linkedList * @author liuyan * @param <E> */public class MyLinkedList<E> implements List<E> {/** * 双向链表结构 */public class LinkNode {// 真正的数据域private E date;// 记录上一个节点private LinkNode prevLinkNode;// 记录下一个节点private LinkNode nextLinkNode;public LinkNode() {}public LinkNode(E date, LinkNode prevLinkNode, LinkNode nextLinkNode) {this.date = date;this.prevLinkNode = prevLinkNode;this.nextLinkNode = nextLinkNode;}}// 结点个数private int nodeSize;// 头结点private LinkNode headNode;// 尾巴节点private LinkNode tailNode;public MyLinkedList() {headNode = null;tailNode = null;}/** * 采用尾端元素增加法,增加新元素 */@Overridepublic boolean add(E element) {if (nodeSize == 0) {headNode = new LinkNode(element, null, tailNode);} else {if (tailNode == null) {tailNode = new LinkNode(element, headNode, null);headNode.nextLinkNode = tailNode;nodeSize++;return true;}LinkNode linkNode = tailNode;tailNode = new LinkNode(element, linkNode, null);linkNode.nextLinkNode = tailNode;}nodeSize++;return true;}/** * 根据索引号查找节点 * * @param index * @return */public LinkNode findLinkNodeByIndex(int index) {LinkNode linkNodeNowTemp = headNode;for (int i = 0; i < nodeSize; i++) {if (i == index) {return linkNodeNowTemp;}linkNodeNowTemp = linkNodeNowTemp.nextLinkNode;}return null;}/** * 按索引位置添加元素 */@Overridepublic void add(int index, E element) {if (nodeSize == 0) {add(element);}// 按照元素先建立新的nodeLinkNode linkNodeNew = new LinkNode(element, null, null);// 找到索引处的节点LinkNode linkNodeNowTemp = findLinkNodeByIndex(index);// 找出索引处节点的上一个nodeLinkNode linkNodePrev = linkNodeNowTemp.prevLinkNode;// 上一个节点的下一个节点指向新nodelinkNodePrev.nextLinkNode = linkNodeNew;// 新节点的上一个节点指向原位置节点上一个节点linkNodeNew.prevLinkNode = linkNodePrev;// 新节点的下一个节点指向原位置节点linkNodeNew.nextLinkNode = linkNodeNowTemp;// 原节点的上一个节点指向新节点linkNodeNowTemp.prevLinkNode = linkNodeNew;nodeSize ++;}/** * 清除所有Node元素资源 */@Overridepublic void clear() {LinkNode linkNodeNowTemp = headNode;for (int i = 0; i < nodeSize; i++) {if (linkNodeNowTemp != tailNode && linkNodeNowTemp != headNode) {linkNodeNowTemp = linkNodeNowTemp.nextLinkNode;linkNodeNowTemp.prevLinkNode.nextLinkNode = null;linkNodeNowTemp.prevLinkNode.prevLinkNode = null;linkNodeNowTemp.prevLinkNode.date = null;linkNodeNowTemp.prevLinkNode = null;} else if (linkNodeNowTemp == tailNode) {linkNodeNowTemp.prevLinkNode = null;} else if (linkNodeNowTemp == headNode) {linkNodeNowTemp.nextLinkNode = null;}}headNode = null;tailNode = null;nodeSize = 0;}/** * 是否包含此元素 */@Overridepublic boolean contains(Object object) {LinkNode linkNodeNowTemp = headNode;for (int i = 0; i < nodeSize; i++) {if (object == linkNodeNowTemp.date) {return true;}linkNodeNowTemp = linkNodeNowTemp.nextLinkNode;}return false;}@Overridepublic E get(int index) {LinkNode linkNode = findLinkNodeByIndex(index);if (linkNode != null) {return linkNode.date;}return null;}@Overridepublic boolean isEmpty() {return nodeSize == 0;}/** * 删除元素 */@Overridepublic boolean remove(Object o) {LinkNode linkNodeNowTemp = headNode;for (int i = 0; i < nodeSize; i++) {if (linkNodeNowTemp.date == o) {if (linkNodeNowTemp != tailNode && linkNodeNowTemp != headNode) {LinkNode linkNewPrev = linkNodeNowTemp.prevLinkNode;LinkNode linkNewNext = linkNodeNowTemp.nextLinkNode;linkNewPrev.nextLinkNode = linkNewNext;linkNewNext.prevLinkNode = linkNewPrev;linkNodeNowTemp.nextLinkNode = null;linkNodeNowTemp.prevLinkNode = null;linkNodeNowTemp.date = null;linkNodeNowTemp = null;nodeSize--;return true;} else if (linkNodeNowTemp == tailNode) {tailNode = linkNodeNowTemp.prevLinkNode;linkNodeNowTemp.prevLinkNode = null;linkNodeNowTemp.date = null;linkNodeNowTemp = null;nodeSize--;return true;} else if (linkNodeNowTemp == headNode) {headNode = linkNodeNowTemp.nextLinkNode;linkNodeNowTemp.nextLinkNode = null;linkNodeNowTemp.date = null;linkNodeNowTemp = null;nodeSize--;return true;}}linkNodeNowTemp = linkNodeNowTemp.nextLinkNode;}return false;}/** * 删除位置标记下的元素 */@Overridepublic E remove(int index) {LinkNode linkNodeNowTemp = headNode;for (int i = 0; i < nodeSize; i++) {if (index == i) {LinkNode linkNewPrev = linkNodeNowTemp.prevLinkNode;LinkNode linkNewNext = linkNodeNowTemp.nextLinkNode;linkNewPrev.nextLinkNode = linkNewNext;linkNewNext.prevLinkNode = linkNewPrev;linkNodeNowTemp.nextLinkNode = null;linkNodeNowTemp.prevLinkNode = null;linkNodeNowTemp.date = null;linkNodeNowTemp = null;break;}linkNodeNowTemp = linkNodeNowTemp.nextLinkNode;}return null;}@Overridepublic int size() {// TODO Auto-generated method stubreturn nodeSize;}@Overridepublic String toString() {StringBuffer str = new StringBuffer("[");LinkNode linkNode = null;for (int i = 0; i < nodeSize; i++) {linkNode = findLinkNodeByIndex(i);str.append("[" + linkNode.date + "],");}if (nodeSize > 0) {return str.substring(0, str.lastIndexOf(",")) + "]";}return str.append("]").toString();}}?和顺序实现一样,实现了核心方法,测试代码相同。
6.?????? 总结
这次总结了线性表的数据结构,并且用数组和双向链表节点实现了类似ArrayList和LinkedList的功能。主要是实现了核心的方法。为了节省资源,一般使用ArrayList存储,但是添加、删除元素的时候就比较费时间,还得移动剩余元素的物理位置,使之物理连续。而双向链表的实现也不是什么省油的灯,占用资源比数组大很多,但是作为经常修改的元素集合,双向链表还是比顺序链表有性能上的优势的。
?