斐波纳契数列(Fibonacci Sequence)
斐波纳契数列(Fibonacci Sequence)

0.前言
很久以前就想写一些竞赛学习的总结,但是由于之前事情比较多,导致计划不断的减缓。现在,大学教学任务的考试已经全部结束了,而比赛也告一段落,所以有时间来整理一下之前学过的东西。不久前,在做比赛的时候遇到了这样一个问题:求出第N个斐波纳契数的前M位和后K位。所以就将斐波纳契数列(Fibonacci Sequence)作为第一步吧。(后面我简称斐波那契数列为Fib,函数Fib(x),代表第x个斐波那契数)
1.从兔子说起
问题:一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔都不死,那么一年以后可以繁殖多少对兔子?
解: 幼仔对数 = 前月成兔对数
成兔对数 = 前月成兔对数+前月幼仔对数
总体对数 = 本月成兔对数+本月幼仔对数
得到通向公式:an+2 = an+1 + an,a1 = a2 = 1
这就是Fib的由来和递推公式的计算。
2.Fib的计算1:递推公式
利用递推公式:Fib(n+2) = Fib(n+1) + Fib(n),Fib(1) = Fib(2) = 1
可以直接想到最简单的计算方法,递归运算。
代码:
其中这个可以用数学归纳法简单的证明,这里就不做证明。
然后我们把上面的快速幂算法应用到矩阵中,就得到了一个对数级的Fib算法。
代码:
其正确性可以通过数学归纳法证明。
这里我们又回到了快速幂的计算上来了。
代码:
这个可以用通向公式简单的证明。在做二分查找的时候可以利用黄金比例分为而不是对半分割,可能会效率更高。
自然界中对于黄金分割的诠释无处不在,最后在这里贴几张图片来感受一下他的神奇:
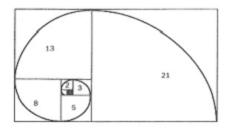
这两张图片是从下面的图片中抽象出来的: