非参数技术之Parzen 窗方法
对一个连续函数P(X)，满足以下性质
（1）X在（a,b）之间的概率如下：
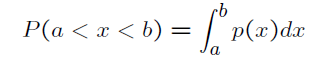
(2)对所有的实数X均满足
P(X)>=0
(3)且满足
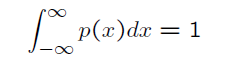
扩展以上概念到向量X
(1)X在区域R上的积分为
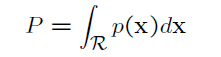
(2)且满足
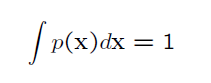
给定一组数量为N的样本，X1，X2，X3，...Xn，对新给定的X我们要估计P(X)的值，我们称这个叫做密度估计。
一个向量落在区域R中的概率为
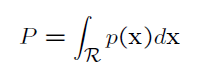
假设区域R很窄，我们有
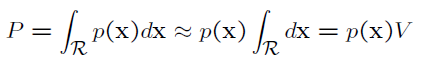
V称作区域R的“体积”
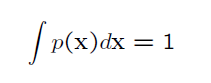
给定一组数量为N的样本，X1，X2，X3，...Xn，对新给定的X我们要估计P(X)的值，我们称这个叫做密度估计。
一个向量落在区域R中的概率为
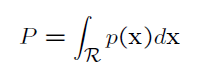
假设区域R很窄，我们有
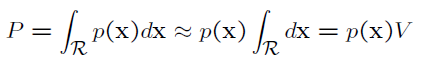
V称作区域R的“体积”。若R是二维的，则V是其宽度，三维的，为面积。
若样本X1，X2，...Xn都是独立的话，那么，假设有k个落在区域R内的话，我们有
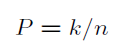
进一步可推导出
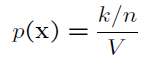
假设R是一个d维的超立方体，h代表超立方体的边长，如下图所示：
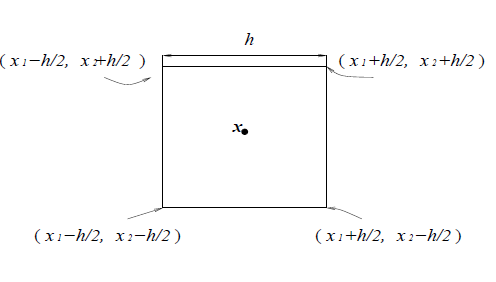
我们引入如下的窗函数
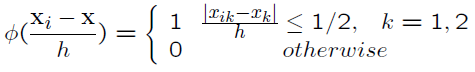
这个窗函数表示，Xi是否在以X为中心，边长为h的正方形中，我们得到
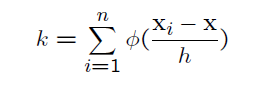
The Parzen probability density estimation formula (for 2-D) is given by
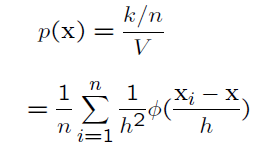
我们可以将窗体函数换成其他的形式，比如换成高斯分布：
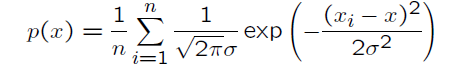
这是在一维情况下的
Example: Given a set of five data points x1 =2, x2 = 2.5, x3 = 3, x4 = 1 and x5 = 6, find Parzen probability density function (pdf) estimates at x = 3, using the Gaussian function with
= 1 as window function.
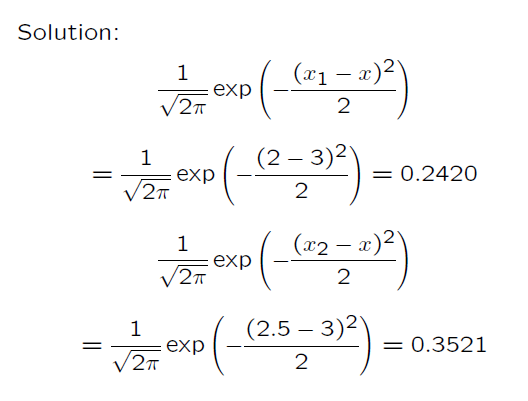
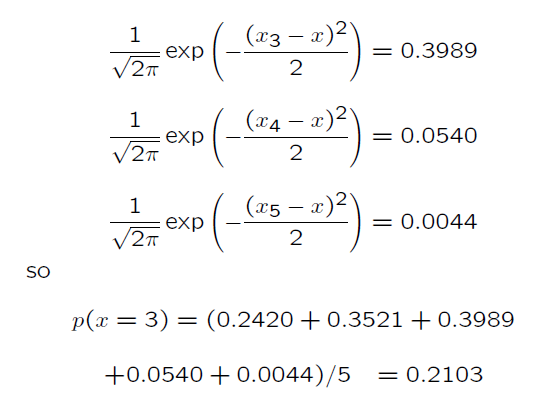
其含义如下图所示
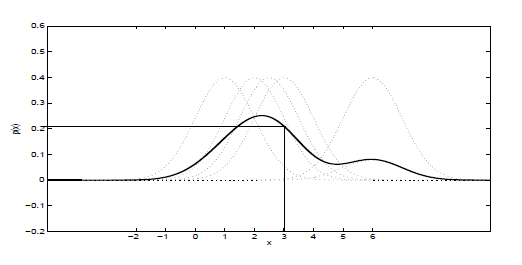
虚线表示分别以x1,x2,x3,x4,x5为中心点的高斯分布，实线是这5个高斯分布叠加之后，在y除以5得到的效果。
最后我想说说关于窗体函数选择的问题：
因为p（x）要满足非负，以及要保证积分结果为1，通过计算可知，我们只要让窗体函数，满足下列性质即可：
（1）非负性
（2）在其定义域上的积分为1
另外，我们可以看出体积V，对p（x）的影响，当v比较小时，大都数的体积均为空，而且，每个邻居的贡献都很清楚，有较大的误差，但当V较大时，平滑效应会很严重，所以选择V成为Parzen窗体的一个限制性问题。
