树的底层实现（上）——平衡树

树的底层实现（下）——平衡树
1.平衡树的定义及构建方法

         平衡树（balanced search tree）：任何节点的左右子树的高度差不大于1。平衡树给人的第一印象是扁平，h维持在O（lgN），所以查找很方便。

         有多种方法构建平衡树，例如下面介绍的“通过有序序列构建”“DSW算法”“AVL tree”

         首先对数进行排序，然后依次去最中间的树一步一步构建，示意图如下

一系列数：2,8,4,9,3,20,5,13,11

排序后：2,3,4,5,8,9,11,13,20

（1）首先取8：2,3,4,5,8,9,11,13,20

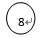
（2）取8左边的中间数3：2,3,4,5,8,9,11,13,20

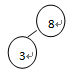
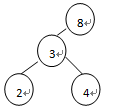
（3）取3左边的中间数2和右边的中间数4

DSW算法分两个阶段：

（1）将任意一颗二叉树通过一系列右旋转（right rotation）生成一棵单链结构（称作vine，即每个非叶结点只有右孩子，没有左孩子）

（2）第二阶段：首先只将一部分节点左旋转，（这算是第一批次左旋转），然后依次对剩下的单链点做多次左旋转（每个批次的左旋转所针对的节点位于剩下的vine上依次相隔的一个节点），直到某个批次的左旋转次数不大于1

具体的代码实现可参考这篇博客：http://blog.csdn.net/cdl2008sky/article/details/6876785

AVL树：左子树和右子树的高度差小于1。从定义上看AVL树的定义与平衡树的定义相同，实际上AVL也包含了balancing the tree的技术。

AVL树一般是对已有树进行调整（restructuring），以达到平衡。分为两种情况：

（1）树的外侧偏高：直接进行单旋转。下例中插入了12后，右外不平衡。

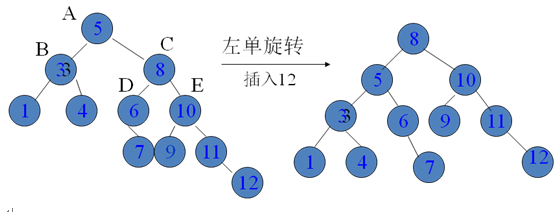
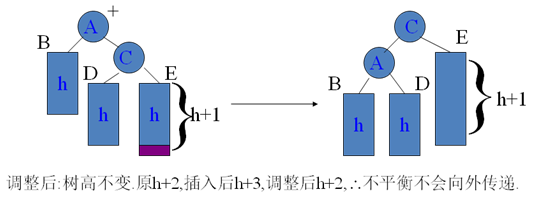
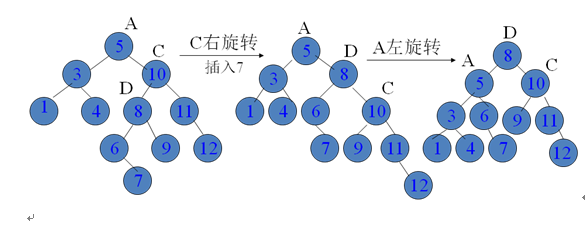
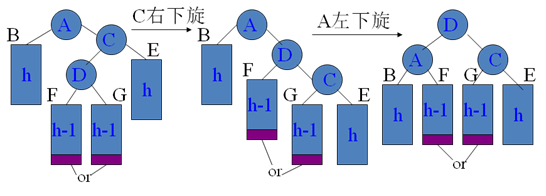
（2）树的内侧增高，下例中，c子树的内侧加高后，需要进行两次旋转。

         在平衡树中，当进行了插入和删除操作后，如果树的平衡收到了威胁，则我们会采取措施恢复平衡，像上面提出的“DSW”方法重新构建树，或者“AVL”对树进行调整。但是有时候，我们会问：重组树是必要的么？因为相对于树的样子，我们更看重是检索到目标节点的速度。为了满足更快检索，提出了优先树。优先树：节点的操作次数越多，所处的位置越接近根节点。

（1）关于节点的计数器

优先树里的节点包含有计数器：记录该节点用于任何操作的次数，于是可以根据计数器来决定节点的位置

（2）如何调整位置

单旋转：被操作的节点与parent换位置，这样下次访问比上次更快。

移动到root：这样做的假设是该节点很可能会被再次访问