【圆满匹配-KM算法】HDU总结

【完美匹配-KM算法】HDU总结
KIDx 的解题报告
题目链接：http://acm.hdu.edu.cn/diy/contest_show.php?cid=12698



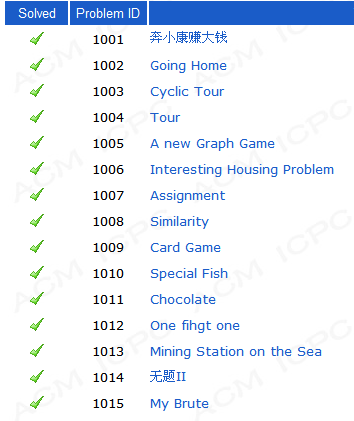
首先献上模板：

#define M 505#define inf 0x3fffffffbool sx[M], sy[M];int match[M], w[M][M], n, m, d, lx[M], ly[M];//n：左集元素个数； m：右集元素个数void init (){    memset (w, 0, sizeof(w));    //不一定要，求最小值一般要初始化为负无穷！}bool dfs (int u){int v; sx[u] = true;for (v = 0; v < m; v++){if (!sy[v] && lx[u]+ly[v]==w[u][v]){sy[v] = true;if (match[v] == -1 || dfs (match[v])){match[v] = u;return true;}}}return false;}int KM (){int i, j, k, sum = 0;memset (ly, 0, sizeof(ly));for (i = 0; i < n; i++){lx[i] = -inf;for (j = 0; j < m; j++)if (lx[i] < w[i][j])lx[i] = w[i][j];}memset (match, -1, sizeof(match));for (i = 0; i < n; i++){while (1){memset (sx, false, sizeof(sx));memset (sy, false, sizeof(sy));if (dfs (i))break;d = inf;for (j = 0; j < n; j++)if (sx[j])for (k = 0; k < m; k++)if (!sy[k])d = min (d, lx[j]+ly[k]-w[j][k]);if (d == inf)    //找不到完美匹配return -1;for (j = 0; j < n; j++)if (sx[j])lx[j] -= d;for (j = 0; j < m; j++)if (sy[j])ly[j] += d;}}for (i = 0; i < m; i++)if (match[i] > -1)sum += w[match[i]][i];return sum;}

第一题：http://acm.hdu.edu.cn/showproblem.php?pid=2255
直接输入w[i][j]边权值建图套模板就可以了

第二题：http://acm.hdu.edu.cn/showproblem.php?pid=1533
将m的坐标记录到左集，h的坐标记录到右集，w[i][j]表示第i个m到第j个h的距离
w[i][j]=△x+△y 然后因为是求最小值，而KM是求最大值
所以只要这样：w[i][j] = -w[i][j]建图再套模板输出【-sum】就ok！

第三题：http://acm.hdu.edu.cn/showproblem.php?pid=1853
直接建图，注意有重边哦！
if (-c > w[a][b])
    w[a][b] = -c;
当木有完美匹配输出-1

第四题：http://acm.hdu.edu.cn/showproblem.php?pid=3488
跟第三题几乎一样

第五题：http://acm.hdu.edu.cn/showproblem.php?pid=3435
跟第三题代码基本上一样，只是要双向建图，也有重边

第六题：http://acm.hdu.edu.cn/showproblem.php?pid=2426
左集是学生，右集是房子，注意 w[i][j] < 0 不可匹配，最后无法完美匹配输出-1

第七题：http://acm.hdu.edu.cn/showproblem.php?pid=2853
题目要求匹配最大值和至少要改变多少个原有匹配
思路：让原有匹配更有优势就可以了
实现：所有权值扩大100倍，原有匹配【例如a匹配b】w[a][b]++
设结果是res
最大值：res/100
至少改变个数：n - res%100

第八题：http://acm.hdu.edu.cn/showproblem.php?pid=3718
题目求的是两字符串的最大相似度
思路：因为第一个串的一种字母只能匹配第二个串的一种字母，所以可以转化为求
【字母的最大匹配值/n】
建图：【例】



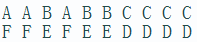
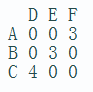
第九题：http://acm.hdu.edu.cn/showproblem.php?pid=3722
直接按题目要求建图，注意跟自己匹配的值是0，w[i][i]=0

第十题：http://acm.hdu.edu.cn/showproblem.php?pid=3395
直接按题目要求建图就可以了

第十一题：http://acm.hdu.edu.cn/showproblem.php?pid=2282
建图：多余的1分别跟所有的0算出最小距离，例如3，多了2个1，要把他们跟所有0匹配，左集是1，右集是这n个数【限制匹配条件（=0）就可以了】
左集个数为m，表示有多少个1需要移动
m = 0；
for (i = 0; i < n; i++)
{
    if (a[i] > 1)
    {
        for (j = 1; j < a[i]; j++)
        {
            for (k = 0; k < n; k++)
                if (a[k] == 0)
                    w[m][k] = -min (abs(k-i), n-abs(k-i));
            m++;
        }
    }
}

第十二题：http://acm.hdu.edu.cn/showproblem.php?pid=2813
这题比较容易超时……
用STL的map把字符串映射为序号
m1.clear();
m2.clear();
k1 = k2 = 1;
while (q--)
{
    scanf ("%s%s%d", s, p, &x);
    string a(s);
    string b(p);
    if (m1[a] == 0)
        m1[a] = k1++;
    if (m2[b] == 0)
        m2[b] = k2++;
    w[m1[a]][m2[b]] = -x;
}

第十三题：http://acm.hdu.edu.cn/showproblem.php?pid=2448
这题要读懂题目意思！
题意：n艘船要分别回到n个码头，另外有m个采矿点，一开始n艘船所在采矿点已经给出，采矿点与采矿点之间给出k条路【双向的】，码头与采矿点之间给出p条路，由于船进入码头后就不会出来，所以这条路是单向的！
实现：最短路+KM

第十四题：http://acm.hdu.edu.cn/showproblem.php?pid=2236
题意：n×n的矩阵中，没行找一个元素，每个元素之间不可同列，求这n个元素的最大值-最小值的最小差
思路：暴力枚举差值【由于元素的值0<= x <=100， 差值的范围也只能是[0,100]】
匈牙利检验就可以了
bool KM (int low, int high)
{
    int i;
    memset (match, -1, sizeof(match));
    for (i = 0; i < n; i++)
    {
        memset (vis, false, sizeof(vis));
        if (!dfs (i, low, high))
            return false;
    }
    return true;
}

第十五题：http://acm.hdu.edu.cn/showproblem.php?pid=3315
默认匹配是w[i][i]
si打赢xj，w[i][j] = v[i]
如果si输了，w[i][j] = -v[i]
所有权值扩大100倍，w[i][i]++优先匹配
相似度=(res%100*100/n)%
踩踩更健康 3 楼 lijunle 2012-05-30   KIDx大神，我想问下，第14题。我用二分+枚举差值，跑最快也要900+ms。你的枚举差值就行的思路是什么意思？为什么你的代码跑得这么快？ 4 楼 基德KID.1412 2012-05-30   lijunle 写道KIDx大神，我想问下，第14题。我用二分+枚举差值，跑最快也要900+ms。你的枚举差值就行的思路是什么意思？为什么你的代码跑得这么快？
先将矩阵中的元素不重复地存放到num数组中，然后枚举
for (i = 0; i <= 100; i++)
    for (j = 0; j < k; j++)
        if (KM (num[j], num[j]+i))
            goto end;

查看更多 下一篇