排列组合-安插算法

排列组合-插入算法
排列组合-插入算法
1.问题描述
    将字符'1','2','2','3','4'的所有的组合用一个算法排列出来。
2.问题分析
    这是一个排列问题，排列个数与参与排列的元素个数有关。假设参与排列的元素个数
为n，那么排列数等于n的阶乘，即F（n）=n!。n! = 1 * 2 * 3 * ... * n.
本文问题描述中出现了重复元素，最后排列中有很多重复的排列需要去掉。本文介绍一种插入算法来解决这个问题。
所有的插入算法的一个共同点：从最小问题单元开始递推。
结合下面的图示开始递推。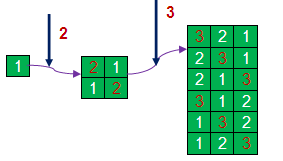

图2-1
    (1)当只有一个元素时，排列数为1，即一种排列。排列：[1]
    (2)当有两个元素时，排列数为2。排列：[2,1],[1,2]
    (3)当有三个元素时，排列数为1 * 2 * 3 = 6。排列：[3,2,1],[2,3,1],[2,1,3],[3,1,2],[1,3,2],[1,2,3]
    ......
    以此类推。
3.算法实现
将一个字符查到一个排列字符数组中：

new char[]{'1','2','3','4','2','2','2'}结果：5040,210    ......

    通过逐一排列的过程可知，在排列中所有对于一个元素的所有重复元素在排列中的任何位置的机会概率是均等的。假设只有一个元素重复，则一个元素重复m次（总共有m+1个元素）后最终的排列数为F(n)= n!/(m+1)!。
5.总结
    通过本文的学习，大家至少知道了一种排列的算法【插入算法】。但这不是最重要的，重要的是学会如何去分析，分解问题。将复杂问题简单化，找到其最小问题单元。从最简单的入手。因为人本身的Memory，CUP和Hard与计算机相比极为有限，并且这种差距还在与日俱增。所以我们只能先处理好最简单的最基本的问题，在接触计算机帮助我们处理复杂问题。

查看更多 下一篇