经典算法大总结之排序算法
从本章开始,我们将总结常用的排序算法
一,插入排序,O(n2)
#include<iostream>using namespace std;void insertionSort(int* A,int len){for(int j=1;j<len;j++){int key = A[j];int i = j-1;while(i>=0&&A[i]>key){A[i+1] = A[i];i = i-1; }A[i+1] = key;}};void main(){ int A[6] = {5,2,4,6,1,3}; insertionSort(A,6); for(int i = 0;i<6;i++) cout<<A[i]<<",";}二,归并排序(C++),O(nlgn)
#include<iostream>#include<vector>using namespace std;void merge(int* A,int p,int q,int r){int n1 = q-p+1;int n2 = r-q;int i,j;vector<int> L(n1+1);vector<int> R(n2+1);for(i=0;i<n1;i++) L[i] = A[p+i];for(j=0;j<n2;j++)R[j] = A[q+j+1];L[n1] = INT_MAX;R[n2] = INT_MAX;i=0;j=0;for(int k =p;k<=r;k++){if(L[i]<=R[j])A[k] = L[i++];elseA[k] = R[j++];}}void mergeSort(int* A,int p,int r){int q = 0;if(p<r){q = (p+r)/2;cout<<q<<endl;mergeSort(A,p,q);mergeSort(A,q+1,r);merge(A,p,q,r);}}void main(){int A[6] = {5,2,4,6,1,3};mergeSort(A,0,5);for(int i = 0;i<6;i++)cout<<A[i]<<",";}二,堆排序(C++),O(nlgn)
堆数据结构是一种数组对象,他可以被视为一棵完全二叉树。树中每个结点与数组中存放该节点值的那个元素对应。
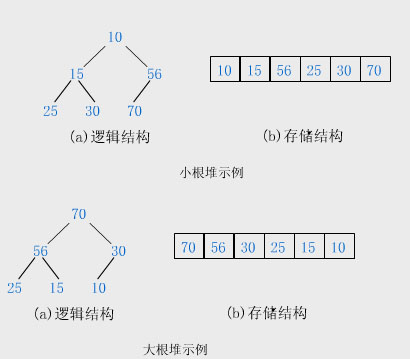
#include <iostream>#include <vector>using namespace std;//保持堆的形态void max_heapify(vector<int> &A,int i,int heap_size){int l=2*i;int r=2*i+1;int largest;if(l<heap_size&&A[l]>A[i])largest = l;elselargest = i;if(r<heap_size&&A[r]>A[largest])largest =r;if(largest != i){int temp = A[i];A[i] = A[largest];A[largest] = temp;max_heapify(A,largest,heap_size);}}//建堆void buidMaxHeap(vector<int> &A){int heap_size = A.size();for(int i = 10/2-1;i>=0;--i)max_heapify(A,i,heap_size);}//堆排序void heapSort(vector<int> &A){buidMaxHeap(A);int heap_size = A.size();for(int i = A.size()-1;i>=1;--i){int temp=A[0];A[0] = A[i];A[i] = temp;--heap_size;max_heapify(A,0,heap_size);}}void main(){int a[10] = {10,9,8,7,6,5,4,3,2,1};vector<int> A(a,a+10);for(int i = 0; i<A.size();++i)cout<<A[i]<<","<<endl;heapSort(A);for(int i = 0; i<A.size();++i)cout<<A[i]<<",";}三,快速排序(C++),O(nlgn)
下面将介绍四种快熟排序的方法:
/*第一种是最初始的快排:Hoare快排*/ #include<iostream>#include<cstdio>using namespace std; int kp[10] = {2, 8, 7, 1, 3, 5, 6, 4};const int size = 8; void print() { for (int i = 0; i < size; i++) {printf("%d ", kp[i]); } puts("");} //一趟快排之后,以枢纽为分隔,左边的<=枢纽, 右边的>=枢纽int Partition(int kp[], int low, int high) { int pivotkey = kp[low];//选定枢轴 while (low < high) { //比枢纽小的交换到低端 while (low < high && kp[high] >= pivotkey) high--; swap(kp[low], kp[high]); //比枢纽大的交换到高端 while (low < high && kp[low] <= pivotkey) low++; swap(kp[low], kp[high]); } return low;}//Partition void Qsort(int kp[], int low, int high) { if (low < high) { int pivotloc = Partition(kp, low, high); //分治思想,递归排序 Qsort(kp, low, pivotloc - 1); Qsort(kp, pivotloc + 1, high); }}//Qsort int main() { puts("原始序列:"); print(); Qsort(kp, 0, size - 1); puts("排序后:"); print(); return 0;}#include <iostream>#include <vector>#include <algorithm>using namespace std;int partition(vector<int> &A,int p,int r){int x = A[r];int i=p-1;int temp;for(int j = p;j<r;++j){if(A[j]<=x){++i;swap(A[i],A[j]);}}swap(A[i+1],A[r]);return i+1;}void quickSort(vector<int> &A,int p,int r){if(p<r){int q = partition(A,p,r);quickSort(A,p,q-1);quickSort(A,q+1,r);}}void main(){int a[10] = {10,9,8,7,6,5,4,3,2,1};vector<int> A(a,a+10);quickSort(A,0,9);for(int i = 0;i<10;++i){cout<<A[i]<<",";}} #include <iostream>#include <vector>#include <algorithm>using namespace std;int partition(vector<int> &A,int p,int r){int x = A[r];int i=p-1;int temp;for(int j = p;j<r;++j){if(A[j]<=x){++i;swap(A[i],A[j]);}}swap(A[i+1],A[r]);return i+1;}inline int Random(int low, int high) { return (rand() % (high - low + 1)) + low;} int Randomized_Partition(vector<int> &kp, int low, int high) { int i = Random(low, high); swap(kp[high], kp[i]); return partition(kp, low, high);}void randomized_quickSort(vector<int> &A,int p,int r){if(p<r){int q = Randomized_Partition(A,p,r);randomized_quickSort(A,p,q-1);randomized_quickSort(A,q+1,r);}}void main(){int a[10] = {9,10,8,7,6,5,4,3,2,1};vector<int> A(a,a+10);randomized_quickSort(A,0,9);for(int i = 0;i<10;++i){cout<<A[i]<<",";}}
第四种 三数中分割法
一组N个数的中值是第[N/2]个最大的数。枢纽元的最好的选择是数组的中值。可是,这很难算出来,并且会明显减慢快速排序的速度。这样的中值的估计可以通过随机选取三个元素并用它们的中值作为枢纽元而得到。事实上,随机性并没有多大的帮助,因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。显然使用三数中值分割法消除了预排序输入的不好情形。
int Median(int kp[], int low, int high) { int center = (low + high) >> 1; if (kp[low] > kp[center]) swap(kp[low], kp[center]); if (kp[low] > kp[high]) swap(kp[low], kp[high]); if (kp[center] > kp[high]) swap(kp[center], kp[high]); swap(kp[center], kp[high - 1]);//枢纽放到了kp[high - 1] return kp[high - 1];}
上面我们已经介绍了几种能在O(nlgn)时间内排序n个数的算法。合并排序和堆排序在最坏情况下都能达到此上界,快速排序在平均情况下达到此上界,下面我们将讨论三种线性时间运行的算法:计数排序,基数排序和堆排序。
三,计数排序:
元素必须是大于等于0,同时不能太大,否则数组res会暴栈
特点是:非常稳定
计数排序的基本思想就是对每一个输入元素x,确定出小于x的元素个数。有了这一信息,就可以把x直接放到它的最终输出数组中的位置上。当以几个元素相同时,这个方案要略作修改,因为不能把它们放在同一个输出位置上。
运行时间为:O(n)
#include <iostream>#include <vector>using namespace std;vector<int> counting_sort(vector<int> A,int k){vector<int> C(++k);vector<int> B(A.size());for(int j = 0;j<A.size();j++)C[A[j]] = C[A[j]]+1;for(int i = 1;i <k;++i)C[i] = C[i] +C[i-1];for(int j = A.size()-1;0<=j;--j){B[--C[A[j]]] = A[j];}return B;}void main(){int a[10] = {9,2,3,4,5,5,1,7,8,10};vector<int> A(a,a+10);vector<int> B = counting_sort(A,10);for(int i= 0;i<B.size();++i)cout<<B[i]<<",";}四、基数排序
排序过程即:先按个位数排序,然后按十位数排序,然后百位数排序,类推……
#include<iostream>using namespace std;#include <vector>int data[10]={73, 22, 93, 43, 55, 14, 28, 65, 39, 81};int tmp[10];int count[10];int maxbit(int data[],int n){ int d=1; for(int i=0;i<n;i++) { int c=1; int p=data[i]; while(p/10) { p=p/10; c++; } if(c>d) d=c; } return d;}void RadixSort(int data[],int n){ int d=maxbit(data,n); int r=1; for(int i=0;i<d;i++){//用计数排序对每一位进行排序 for(int k=0;k<10;k++) count[k]=0; for(int j=0;j<n;j++) { int k=data[j]/r; int q=k%10; count[q]++; } for(int j=1;j<10;j++) { count[j]+=count[j-1]; } for(int j=n-1;j>=0;j--) { int p=data[j]/r; int s=p%10; tmp[--count[s]]=data[j]; } for(int j=0;j<n;j++) { data[j]=tmp[j]; } r=r*10; }}int main(){ cout<<"基数排序c++实现"<<endl; cout<<maxbit(data,10)<<endl; cout<<"排序之前的数值:"; for(int i=0;i<10;i++) cout<<data[i]<<" "; cout<<endl; RadixSort(data,10); cout<<"排序之后的数值:"; for(int i=0;i<10;i++) cout<<data[i]<<" "; cout<<endl; return 0;}五、桶排序
桶排序的思想就是把区间[0,1)划分为n个相同大小的子区间,或称桶。然后,将n个输入数分布到各个桶中去。为得到结果,先对各个桶中的数进行排序,然后按次序把各桶中的元素列出来即可。
1.#include<iostream.h> 2.#include<malloc.h> 3. 4.typedef struct node{ 5. int key; 6. struct node * next; 7.}KeyNode; 8. 9.void inc_sort(int keys[],int size,int bucket_size){ 10. KeyNode **bucket_table=(KeyNode **)malloc(bucket_size*sizeof(KeyNode *)); 11. for(int i=0;i<bucket_size;i++){ 12. bucket_table[i]=(KeyNode *)malloc(sizeof(KeyNode)); 13. bucket_table[i]->key=0; //记录当前桶中的数据量 14. bucket_table[i]->next=NULL; 15. } 16. for(int j=0;j<size;j++){ 17. KeyNode *node=(KeyNode *)malloc(sizeof(KeyNode)); 18. node->key=keys[j]; 19. node->next=NULL; 20. //映射函数计算桶号 21. int index=keys[j]/10; 22. //初始化P成为桶中数据链表的头指针 23. KeyNode *p=bucket_table[index]; 24. //该桶中还没有数据 25. if(p->key==0){ 26. bucket_table[index]->next=node; 27. (bucket_table[index]->key)++; 28. }else{ 29. //链表结构的插入排序 30. while(p->next!=NULL&&p->next->key<=node->key) 31. p=p->next; 32. node->next=p->next; 33. p->next=node; 34. (bucket_table[index]->key)++; 35. } 36. } 37. //打印结果 38. for(int b=0;b<bucket_size;b++) 39. for(KeyNode *k=bucket_table[b]->next; k!=NULL; k=k->next) 40. cout<<k->key<<" "; 41. cout<<endl; 42.} 43. 44.void main(){ 45. int raw[]={49,38,65,97,76,13,27,49}; 46. int size=sizeof(raw)/sizeof(int); 47. inc_sort(raw,size,10); 48.} 六 各种排序算法的比较:
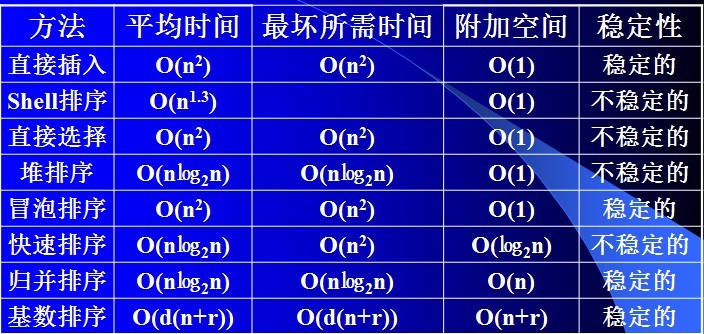
排序稳定性的一点知识:
1)稳定的:如果存在多个具有相同排序码的记录,经过排序后,这些记录的相对次序仍然保持不变,则这种排序算法称为稳定的。
插入排序、冒泡排序、归并排序、分配排序(桶式、基数)都是稳定的排序算法。
2)不稳定的:否则称为不稳定的。
直接选择排序、堆排序、shell排序、快速排序都是不稳定的排序算法。
一个各种排序算法演示网站:http://www.sorting-algorithms.com/ (看网址就知道)