小毛驴的困惑(2)---小驴的爆发一.题外话:首先,小驴不可能带1000胡萝卜直接奔向兔子国,这样到最后不仅一个
小毛驴的困惑(2)---小驴的爆发

一.题外话:
首先,小驴不可能带1000胡萝卜直接奔向兔子国,这样到最后不仅一个没带过去,还会把自己省下的2000胡萝卜弄丢了.
其次,小驴不可能忽然奥特曼附体,一下驼起3000胡萝卜,一口气走了过去,丫的这里是天朝不是日本. 然后,小驴也不可能投箸于席,奋袂而起,半日行军一千里. 最后,小驴更不会装傻卖萌:"啥是胡萝卜啊?" 既然所有办法都行不通,小驴就只好踏踏实实一步一步算了. 二.沉睡的毛利 小学时候曾经遇到过这样的数学题: AB两人分别从甲乙两地同时出发相向而行,甲乙距离为L,而AB两个人的速度为X1,X2,出发时,甲旁边有一条小狗以大于X1,X2的速度X3向乙跑去,遇到乙时候迅速返回再向甲跑去,遇到甲再折回跑向乙,如此反复,问: 甲乙两人相遇时,小狗一共跑了多少距离? 初一看觉得这个问题貌似非常复杂,其实解决这个问题的关键在不要纠结于每次小狗折回奔跑的距离的变化,而要抓住实质性的东西,即: 恒定的速度和奔跑时间. 小驴驼胡萝卜的问题和上面这个问题有异曲同工之妙,小驴每公里吃一根胡萝卜,所以小驴最终剩下的胡萝卜其实取决于小驴走的路程,所以这个问题其实要求的是最短路径. 再回到胡萝卜的问题上来,小驴每次最多驼1000的胡萝卜,每走1km消耗1根胡萝卜,要想活下命来,它每次走的距离都应在1000根胡萝卜的消耗内,由于出发时候胡萝卜总量大于1000,所以小驴必须走到一个距离出发点为X的地方折回搬剩下的胡萝卜,由此我们得到第一个条件: 2X<1000km (a) 显然(a)这个条件是远远不够解决问题的,一共3000根胡萝卜,求的这个问题的关键就在于意识到,既然求最小消耗,就在第一个1000根胡萝卜消耗完的时候完成对3000根胡萝卜的第一次搬迁.让我们对小驴消耗第一个1000根胡萝卜这个过程仔细分析一下:
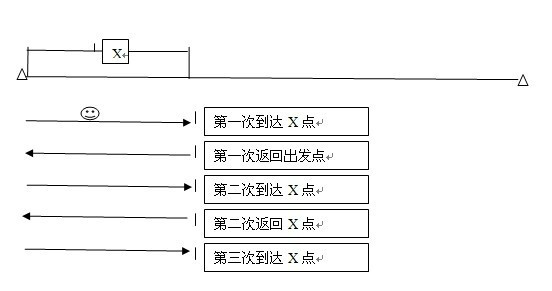
1: 小驴出发时候先拖1000根胡萝卜到X点,消耗X根胡萝卜,X点剩余1000-X 2. 小驴带X根胡萝卜返回出发点, X点剩余1000-2x 3. 小驴驼1000胡萝卜到X点,消耗X根, X点剩余2000-3X 4. 小驴带X根胡萝卜返回出发点,X点剩余2000-4X 5. 小驴驼1000胡萝卜到X点,消耗X根, X点剩余 3000-5X. 由于是在消耗第一个1000根胡萝卜的时候到达X点,即最后剩余应为2000胡萝卜,所以有 5X=1000 -->X=200 即小驴应第一次在距离出发点200km的地方停留. 然后小驴从X点继续出发,由于剩余2000根胡萝卜,小驴不能一次驼完,所以与过程以相似,只不过这次小驴只需要两次就可以驼完,假设第二次停留点为Y点:
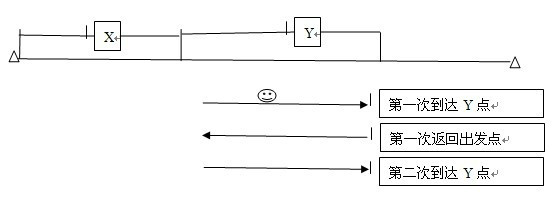
1.小驴第一次出发驼1000胡萝卜到Y点,消耗Y根胡萝卜,Y点剩余1000-Y胡萝卜, 2.小驴第一次返回X点,Y点剩余1000-2Y胡萝卜 3.小驴第二次出发驼1000胡萝卜,到达Y点,消耗Y根胡萝卜,最后Y点剩余2000-3Y胡萝卜和过程一相似,此时有等式 3Y=1000, 即:Y=333.3 此时小驴恰好还剩1000胡萝卜,而距离目的地兔子国还有1000-200-333.3=466.3km 所以这次小驴 可以一次性的驼过去,最后达到兔子国的时候还剩下(1000-466.3)=534根胡萝卜(取整)
三.续集的开始 不过我还有个小小的疑惑,为什么最后要取整534根呢.而不是533捏. 可能小驴是个善良的小驴,最后那不到半公里的路程小驴忍住了饥饿,将多出的一个胡萝卜送给了更需要塔\它的兔子. 好啦,小驴的困惑到此已经结束.它成功将最大量的胡萝卜送到了兔子国,收到了兔子国国王的奖励,小驴对子兴奋异常,关于这个奖励我们下次再谈. 那天小驴在兔子国溜达,在我下班路上遇到了我,由于它很高兴,可能也希望我跟着一块分享它的快乐,于是给我讲了它是如何解决自己的困惑的.我听后也为小驴子有这样的突破欢欣不已,却不料,小驴挠了挠头,一拍大腿,撂了撂蹄子,对我喊: "HI,大猴子,你不是程序猿嘛,你能用你的程序解决我的难题么?" 我作为工业革命的新物种,人类科技研究上的一种重新演变,并且拥有无与伦比的耐力、超越时代的智商、横穿社会的苦逼相和低于人类平均寿命的优良特点,听到这个顿时也很感兴趣,不过今天确实有点晚了,又到了睡觉时间了,明天抽空再来用程序猿的惯用伎俩解决这个问题吧. 小驴打了打哈欠说:"那就明天吧,今天我也困了,要好好休息了,明天我还要呢" 我连忙问:"国王奖励你了什么啊?" 小驴四周瞧了瞧,招呼我凑过来,然后悄悄在我的耳边说:"保密!" 这你丫的!


