破解一道平面镶嵌题
郑州初一年级的数学爱好者中，有位“老大”，跟我一个课外班。我不知道他的名字，只晓得外号“灰太狼”。他把数学当“羊村”，什么几何“羊”、代数“羊”、三角函数“羊”，无论初中的题还是高中的题，都被他玩得团团转。听他妈妈讲，他的本事就是做题做出来的。老师教过的，没教过的，全做，做成明星了。
于是，大伙儿都以他为榜样，使劲地做题。今天，我也找了一道老师没教过的“平面镶嵌”题来做，练练脑子。
求证：用哪几种正多边形（单独用一种）可以进行平面镶嵌？
如果只让说出一种，我随口就能答，因为家里铺的就是四方的地板砖。然而，问哪几种，还让求证，这脑子就成浆糊了。我瞅着地板砖想呀想，突然悟出一个道理：若要无缝平面镶嵌，这正多边形的内角和必须满足一个要求，即能够拼成360°。
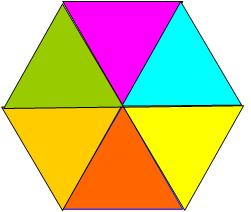我随手画了一幅正三边形镶嵌的图，偶然发现：中点的360°周角除以边数3所得的120°，恰是正三边形一个角的外角的度数；再用平角180°减去120°，就是正三边形一个角的度数。既然正三边形如此，正n边形应当也是如此。于是，我就有了解题思路：
解：设正n边形可以平面镶嵌，k个正n边形内角和为360°。
根据所设，列式：（180°- 360°/ n）× k = 360°
该算式中，360°/
n是正n边形一个角的外角的度数，180°- 360°/ n则是正n边形一个角的度数，再乘以正n边形的个数k，等于360°。接下来，就开始计算：
原式变为180°k
- 360°k / n = 360°，等式两边分别除以180°，成k - 2k / n = 2。等式两边再分别乘以n，则成kn
- 2k = 2n，继而成k（n–2）= 2n。
于是，k =
2n /（n–2）。等式右边的分子2n减去4再加上4，值不变，即为2n–4 + 4,又为2（n–2）+ 4。这样，
k = 2（n–2）/（n–2）+ 4 /（n–2）= 2 + 4 /（n–2）。
至此，我遇上了麻烦。k = 2 + 4 /（n–2）中，有k和n两个未知数，接下来该咋办呢？哦，根据题意，n肯定是个正整数，n–2还必须能被4整除。这就好办了，n–2只能等于1或2或4。若n–2 = 1，n = 3；n–2 = 2，n = 4；n–2 = 4，n = 6。由此，我得出一个结论：用三种正多边形（单独用一种）可以进行平面镶嵌，即正三边形、正四边形和正六边形。
呵，真高兴，我似乎感觉到“灰太狼”向我投来赞许的目光。
