教你透辟了解红黑树（修订版）

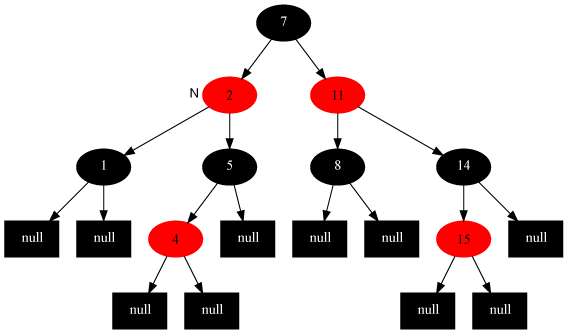
教你透彻了解红黑树（修订版）

此图忽略了叶子和根部的父结点。总之，可以这样表示，就对了。:D。

二、树的旋转知识
当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。
为了保持红黑树的性质，我们可以通过对树进行旋转，即修改树种某些结点的颜色及指针结构，以达到对红黑树进行
插入、删除结点等操作时，红黑树依然能保持它特有的性质（如上文所述的，五点性质）。

树的旋转，分为左旋和右旋，以下借助图来做形象的解释和介绍：
1.左旋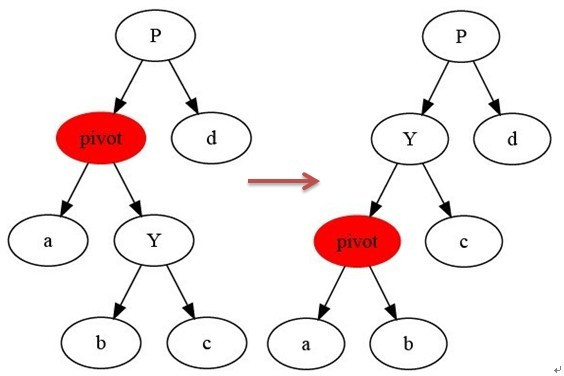


如上图所示：
当在某个结点pivot上，做左旋操作时，我们假设它的右孩子y不是NIL[T]，pivot可以为树内任意右孩子而不是NIL[T]的结点。
左旋以pivot到y之间的链为“支轴”进行，它使y成为该孩子树新的根，而y的左孩子b则成为pivot的右孩子。
 
来看算法导论对此操作的算法实现（以x代替上述的pivot）：

对于树的旋转，能保持不变的只有原树的搜索性质，而原树的红黑性质则不能保持，
在红黑树的数据插入和删除后可利用旋转和颜色重涂来恢复树的红黑性质。

至于有些书如 STL源码剖析有对双旋的描述，其实双旋只是单旋的两次应用，并无新的内容，
因此这里就不再介绍了，而且左右旋也是相互对称的，只要理解其中一种旋转就可以了。


三、红黑树插入、删除操作的具体实现
ok，接下来，咱们来具体了解红黑树的插入操作。
向一棵含有n个结点的红黑树插入一个新结点的操作可以在O（lgn）时间内完成。

算法导论：
RB-INSERT(T, z)
 1  y ← nil[T]
 2  x ← root[T]
 3  while x ≠ nil[T]
 4      do y ← x
 5         if key[z] < key[x]
 6            then x ← left[x]
 7            else x ← right[x] 
 
 8  p[z] ← y
 9  if y = nil[T]
10     then root[T] ← z
11     else if key[z] < key[y]
12             then left[y] ← z
13             else right[y] ← z
14  left[z] ← nil[T]
15  right[z] ← nil[T]
16  color[z] ← RED
17  RB-INSERT-FIXUP(T, z)

咱们来具体分析下，此段代码：
RB-INSERT(T, z)，将z插入红黑树T 之内。

为保证红黑性质在插入操作后依然保持，上述代码调用了一个辅助程序RB-INSERT-FIXUP
来对结点进行重新着色，并旋转。

14  left[z] ← nil[T]
15  right[z] ← nil[T]  //保持正确的树结构
第16行，将z着为红色，由于将z着为红色可能会违背某一条红黑树的性质，
所以，在第17行，调用RB-INSERT-FIXUP（T,z）来保持红黑树的性质。

RB-INSERT-FIXUP(T, z)，如下所示：
 
1 while color[p[z]] = RED
 2     do if p[z] = left[p[p[z]]]
 3           then y ← right[p[p[z]]]
 4                if color[y] = RED
 5                   then color[p[z]] ← BLACK                    ? Case 1
 6                        color[y] ← BLACK                       ? Case 1
 7                        color[p[p[z]]] ← RED                   ? Case 1
 8                        z ← p[p[z]]                            ? Case 1
 9                   else if z = right[p[z]]
10                           then z ← p[z]                       ? Case 2
11                                LEFT-ROTATE(T, z)              ? Case 2
12                           color[p[z]] ← BLACK                 ? Case 3
13                           color[p[p[z]]] ← RED                ? Case 3 
 
14                           RIGHT-ROTATE(T, p[p[z]])            ? Case 3
15           else (same as then clause
                         with "right" and "left" exchanged)
16 color[root[T]] ← BLACK

 
ok，参考一网友的言论，用自己的语言，再来具体解剖下上述俩段代码。
为了保证阐述清晰，我再写下红黑树的5个性质：

1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点，即空结点（NIL）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

在对红黑树进行插入操作时，我们一般总是插入红色的结点，因为这样可以在插入过程中尽量避免对树的调整。
那么，我们插入一个结点后，可能会使原树的哪些性质改变列?
由于，我们是按照二叉树的方式进行插入，因此元素的搜索性质不会改变。

如果插入的结点是根结点，性质2会被破坏，如果插入结点的父结点是红色，则会破坏性质4。
因此，总而言之，插入一个红色结点只会破坏性质2或性质4。
我们的回复策略很简单，
其一、把出现违背红黑树性质的结点向上移，如果能移到根结点，那么很容易就能通过直接修改根结点来恢复红黑树的性质。直接通过修改根结点来恢复红黑树应满足的性质。
其二、穷举所有的可能性，之后把能归于同一类方法处理的归为同一类，不能直接处理的化归到下面的几种情况，

情况1：插入的是根结点。
原树是空树，此情况只会违反性质2。
  对策：直接把此结点涂为黑色。
情况2：插入的结点的父结点是黑色。
此不会违反性质2和性质4，红黑树没有被破坏。
  对策：什么也不做。
情况3：当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色。
此时父结点的父结点一定存在，否则插入前就已不是红黑树。
与此同时，又分为父结点是祖父结点的左子还是右子，对于对称性，我们只要解开一个方向就可以了。

在此，我们只考虑父结点为祖父左子的情况。
同时，还可以分为当前结点是其父结点的左子还是右子，但是处理方式是一样的。我们将此归为同一类。
  对策：将当前节点的父节点和叔叔节点涂黑，祖父结点涂红，把当前结点指向祖父节点，从新的当前节点重新开始算法。

针对情况3，变化前（图片来源：saturnman）：
  变化前：


变化后：


情况4：当前节点的父节点是红色,叔叔节点是黑色，当前节点是其父节点的右子
对策：当前节点的父节点做为新的当前节点，以新当前节点为支点左旋。
如下图所示，变化前：


 变化后：


情况5：当前节点的父节点是红色,叔叔节点是黑色，当前节点是其父节点的左子
解法：父节点变为黑色，祖父节点变为红色，在祖父节点为支点右旋

如下图所示


变化后：



--------------------------------
 ok，接下来，咱们最后来简单了解，红黑树的删除操作：
算法导论一书，给的算法实现： 
RB-DELETE(T, z)
 
1 if left[z] = nil[T] or right[z] = nil[T]
 2    then y ← z
 3    else y ← TREE-SUCCESSOR(z)
 4 if left[y] ≠ nil[T]
 5    then x ← left[y]
 6    else x ← right[y]
 7 p[x] ← p[y]
 8 if p[y] = nil[T]
 9    then root[T] ← x
10    else if y = left[p[y]]
11            then left[p[y]] ← x
12            else right[p[y]] ← x
13 if y 3≠ z
14    then key[z] ← key[y]
15         copy y's satellite data into z
16 if color[y] = BLACK
17    then RB-DELETE-FIXUP(T, x)
18 return y


RB-DELETE-FIXUP(T, x)
 1 while x ≠ root[T] and color[x] = BLACK
 2     do if x = left[p[x]] 
 
 3           then w ← right[p[x]]
 4                if color[w] = RED
 5                   then color[w] ← BLACK                        ?  Case 1
 6                        color[p[x]] ← RED                       ?  Case 1
 7                        LEFT-ROTATE(T, p[x])                    ?  Case 1
 8                        w ← right[p[x]]                         ?  Case 1
 9                if color[left[w]] = BLACK and color[right[w]] = BLACK
10                   then color[w] ← RED                          ?  Case 2
11                        x p[x]                                  ?  Case 2
12                   else if color[right[w]] = BLACK
13                           then color[left[w]] ← BLACK          ?  Case 3
14                                color[w] ← RED                  ?  Case 3
15                                RIGHT-ROTATE(T, w)              ?  Case 3
16                                w ← right[p[x]]                 ?  Case 3
17                         color[w] ← color[p[x]]                 ?  Case 4 
 
18                         color[p[x]] ← BLACK                    ?  Case 4
19                         color[right[w]] ← BLACK                ?  Case 4
20                         LEFT-ROTATE(T, p[x])                   ?  Case 4
21                         x ← root[T]                            ?  Case 4
22        else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK

saturnman：
我们红黑树删除的几种情况：
(注：以下各种情况，不与上述算法导论之上的代码相对应。)
情况1：当前节点是红+黑色
    解法，直接把当前节点染成黑色，结束。
此时红黑树性质全部恢复。

情况2：当前节点是黑+黑且是根节点
    解法：什么都不做，结束

情况3：当前节点是黑+黑且兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑)。
    解法：把父节点染成红色，把兄弟结点染成黑色，之后重新进入算法（我们只讨论当前节点是其父节点左孩子时的情况）。此变换后原红黑树性质5不变，而把问题转化为兄弟节点为黑色的情况。
               3.变化前：
..........

===========
更多请参考：
http://blog.csdn.net/v_JULY_v/archive/2010/12/29/6105630.aspx
详情，参见My BLog：
http://blog.csdn.net/v_JULY_v
     July、12.30凌晨。
[解决办法]
谢谢楼主，学习学习
[解决办法]
不错，收藏~
[解决办法]
好东西，收藏~~
[解决办法]
不错，收藏
[解决办法]
很好，收藏了
[解决办法]
mark一下收藏起来，以后再细细看