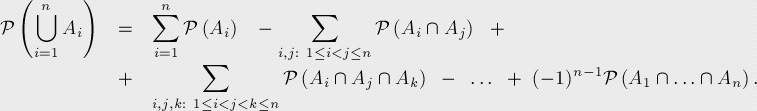容斥原理 专题

http://acm.hdu.edu.cn/showproblem.php?pid=4336

Card Collector

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1410    Accepted Submission(s): 626
Special Judge

Problem DescriptionInputOutputSample InputSample OutputSourceRecommend，代表发生某些事件的概率（即发生其中至少一个事件的概率），则：

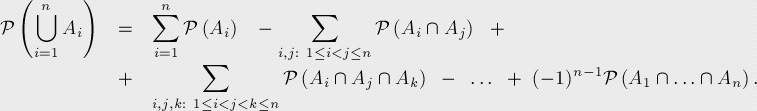
#include<iostream>#include<cstdlib>#include<stdio.h>using namespace std;int n;double p[25];double uu;void dfs(int k,double sum,int cou,int pi){    if(cou==k)    {        uu+=1/sum;        return ;    }    for(int i=pi;i<=n;i++)    {        sum+=p[i];        cou++;        dfs(k,sum,cou,i+1);        sum-=p[i];        cou--;    }    return ;}int main(){    while(scanf("%d",&n)!=EOF)    {        double sum=0;        for(int i=1;i<=n;i++)        {            scanf("%lf",&p[i]);sum+=(1/p[i]);        }        for(int i=2;i<=n;i++)        {            uu=0;            dfs(i,0,0,1);            if(i&1) sum+=uu;            else sum-=uu;        }        printf("%lf\n",sum);    }}

http://acm.hdu.edu.cn/showproblem.php?pid=2461

Rectangles

Time Limit: 5000/4000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1028    Accepted Submission(s): 581

Problem DescriptionInputOutputSample InputSample OutputSourceRecommend#include<iostream>#include<cstdlib>#include<stdio.h>#include<algorithm>using namespace std;int n,m,num,res;int a[25];struct Node{ int x1,y1,x2,y2; int s;}node[25];bool check(Node x,int u){ if(node[u].x1>=x.x2) return 0; if(x.x1>=node[u].x2) return 0; if(node[u].y1>=x.y2) return 0; if(x.y1>=node[u].y2) return 0; return 1;}void solve(Node rec,int id,int k){ Node temp; if(id==num+1) return ; for(int i=id;i<=num;i++) { if(check(rec,a[i])) { temp.x1=rec.x1>node[a[i]].x1?rec.x1:node[a[i]].x1; temp.y1=rec.y1>node[a[i]].y1?rec.y1:node[a[i]].y1; temp.x2=rec.x2<node[a[i]].x2?rec.x2:node[a[i]].x2; temp.y2=rec.y2<node[a[i]].y2?rec.y2:node[a[i]].y2; temp.s=(temp.x2-temp.x1)*(temp.y2-temp.y1); if(k%2) res+=temp.s; else res-=temp.s; solve(temp,i+1,k+1); } }}int main(){ int count=1; while(scanf("%d%d",&n,&m)!=EOF) { if(n==0&&m==0) break; for(int i=1;i<=n;i++) { scanf("%d%d%d%d",&node[i].x1,&node[i].y1,&node[i].x2,&node[i].y2); node[i].s=(node[i].x2-node[i].x1)*(node[i].y2-node[i].y1); } printf("Case %d:\n",count++); for(int i=1;i<=m;i++) { scanf("%d",&num); res=0; for(int j=1;j<=num;j++) { scanf("%d",&a[j]); res+=node[a[j]].s; } for(int j=1;j<=num;j++) { solve(node[a[j]],j+1,0); } printf("Query %d: ",i); printf("%d\n",res); } puts(""); } return 0;}Problem DescriptionInputOutputSample InputSample OutputAuthorSourceRecommend#include<iostream>#include<cstdlib>#include<stdio.h>#define ll __int64using namespace std;int a[15];ll res,n;int m;int gcd(int x,int y){ if(y==0) return x; return gcd(y,x%y);}int lcm(int x,int y){ return x/gcd(x,y)*y;}void dfs(int now,int step,int k){ if(step==m+1) return ; for(int i=step;i<=m;i++) { if(a[i]!=0) { int temp=lcm(now,a[i]);//应该是最小公倍数，而不是乘积，一开始nc了~ int ans=n/temp; if(n%temp==0) ans--; if(k%2) res+=ans; else res-=ans; dfs(temp,i+1,k+1); } }}int main(){ while(scanf("%I64d%d",&n,&m)!=EOF) { res=0; for(int i=1;i<=m;i++) { scanf("%d",&a[i]); if(a[i]!=0) { int num=n/a[i]; if(n%a[i]==0) num--; res+=num; } } for(int i=1;i<=m;i++) { if(a[i]!=0) dfs(a[i],i+1,0); } printf("%I64d\n",res); }}
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3556#include<iostream>#include<cstdlib>#include<stdio.h>using namespace std;#define mm 1000000007typedef long long ll;ll powermod(ll a,ll b){ ll res=1; while(b) { if(b&1)res=(res*a)%mm;//不能写成res*=a%mm~~~~~~~~~ a=a*a; a%=mm; b>>=1; } return res%mm;}int main(){ ll n,k; while(scanf("%lld%lld",&n,&k)!=EOF) { ll ans=powermod(2,k); ans--; ans=powermod(ans,n); printf("%lld\n",ans); }}

http://poj.org/problem?id=1091

#include<iostream>#include<cstdlib>#include<stdio.h>#include<math.h>#define ll __int64using namespace std;ll n,m;ll p[65];ll a[65];int cc;ll ans;void get(){ int i; cc=0; ll mm=m; for(i=2;i*i<=mm;i++) { if(mm%i==0) { p[cc++]=i; while(mm%i==0) mm/=i; } } if(mm>1) p[cc++]=mm;}ll quickpower(ll a,ll b){ ll res=1; while(b) { if(b&1) res*=a; a=a*a; b>>=1; } return res;}void get_sum(int id,int step,int num){ if(step==num) { ll uu=m; for(int i=0;i<step;i++) uu/=a[i]; ans+=quickpower(uu,n); return ; } for(int i=id;i<cc;i++) { a[step]=p[i]; get_sum(i+1,step+1,num); } return ;}int main(){ while(scanf("%I64d%I64d",&n,&m)!=EOF) { get(); ll res=quickpower(m,n); for(int i=1;i<=cc;i++) { ans=0; get_sum(0,0,i); if(i&1) res-=ans; else res+=ans; } printf("%I64d\n",res); }}

http://poj.org/problem?id=3904

//这题很久以前做过了，好久没有接触过容斥了，拿来复习复习//求得是n个数中，有多少组(a,b,c,d)的公约数为1，值得注意的是这四个数不一定两两互质。//所以我们从它的反面考虑，先求出公约数不为1的个数。//思路：把每个数素数分解，记录不重复素因子所能组成的因子，把这些因子的总数统计，并且统计每个因子是由多少个素因子组成//如这n个数中含2的个数为a,含3的个数为b,含6的个数为c,那么公约数大于1的总数为p=c(a,4)+c(b,4)-c(c,4),总的个数为c(n,4)//用c(n,4)-p即为所求#include<iostream>#include<cstdlib>#include<stdio.h>#include<memory.h>using namespace std;#define maxn 10005long long count[maxn];long long num[maxn];long long p[maxn];long long prime[maxn];void init(){ memset(p,0,sizeof(p)); memset(num,0,sizeof(num)); for(long long i=4;i<maxn;i++) p[i]=i*(i-1)*(i-2)*(i-3)/24;}void solve(long long n){ long long tol=0; for(long long i=2;i*i<=n;i++) { if(n%i==0) { prime[tol++]=i; } while(n%i==0) n/=i; } if(n!=1) prime[tol++]=n; for(long long i=1;i<(1<<tol);i++) { long long k=1; long long sum=0; for(long long j=0;j<tol;j++) { if(i&(1<<j)) { k*=prime[j]; sum++; } } count[k]++;//记录当前因子的个数 num[k]=sum;//记录当前因子是由多少个素因子组成 }}int main(){ init(); long long n; long long m; while(scanf("%lld",&n)!=EOF) { memset(count,0,sizeof(count)); for(long long i=0;i<n;i++) { scanf("%lld",&m); solve(m); } long long ans=0; for(long long i=0;i<maxn;i++) { if(count[i]) { if(num[i]%2) { ans+=p[count[i]]; } else ans-=p[count[i]]; } } cout<<p[n]-ans<<endl; }}