集合问题是数量关系中常考的题型之一,无论是近两年的国考,还是省考,都考到了集合问题。
例:某公司招聘员工,按规定每人至多可报考两个职位,结果共42人报名,甲、乙、丙三个职位报名人数分别是22人、16人、25人,其中同时报甲、乙职位的人数为8人,同时报甲、丙职位的人数为6人,那么同时报乙、丙职位的人数为( )。(2012年4.21联考第101题)
A. 7人 B. 6人 C. 5人 D. 8人
让我们先来学习集合问题的解题方法,再做这道例题。
集合问题有两种解法:一种是公式法,一种是图示法。
1.公式法:适用于条件与问题都可直接代入公式的题目。
(1)两个集合:
︱A∪B︱=︱A︱+︱B︱-︱A∩B︱
(2)三个集合:
︱A∪B∪C︱=︱A︱+︱B︱+︱C︱-︱A∩B︱-︱B∩C︱-︱C∩A︱+︱A∩B∩C︱
2. 图意法:用图形来表示集合关系,变抽象文字为形象图示。
例1:
对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有( )。
A.22人 B.28人 C.30人 D.36人
【解析】A。设A=喜欢看球赛的人(58),B=喜欢看戏剧的人(38),C=喜欢看电影的人(52),则有:
A∩B=既喜欢看球赛的人又喜欢看戏剧的人(18)
B∩C=既喜欢看电影又喜欢看戏剧的人(16)
A∩B∩C=三种都喜欢看的人(12)
A∪B∪C=看球赛和电影、戏剧至少喜欢一种(100)
根据公式:A+B+C=A∪B∪C+︱A∩B︱+︱B∩C︱+︱C∩A︱-︱A∩B∩C︱
︱C∩A︱=A+B+C-(︱A∪B∪C︱+︱A∩B︱+︱B∩C︱-︱A∩B∩C︱)
=148-(100+18+16-12)=26
所以,只喜欢看电影的人=C-︱B∩C︱-︱C∩A︱+︱A∩B∩C︱
=52-16-26+12
=22
例2:
外语学校有英语、法语、日语教师共27人,其中只能教英语的有8人,只能教日语的有6人,能教英、日语的有5人,能教法、日语的有3人,能教英、法语的有4人,三种都能教的有2人,则只能教法语的有( )。
A.4人 B.5人 C.6人 D.7人
【解析】B。此题应该用文氏图法,将能教英语、日语、法语的教师分别设为不同的集合。先设所有集合的交集为2,依题意得文氏图(见下图)。
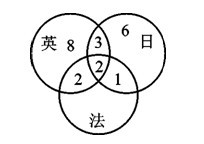
由图可得只能教法语的老师为:27-8-6-3-2-2-1=5人。
例3:
现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做
正确的有31人,两种实验都做错的有4人,则两种实验都做对的有( )。
A.27人 B.25人 C.19人 D.10人