学好数学三部曲(三)
“课后及时复习”
上学的路上,经常听到家长说的最多的一句话:“某某,上课要认真听讲。”殊不知,课堂上认真听课对学生来说至关重要,课后及时复习也同样重要。心理学表明:记忆时,先摄入大脑的内容会对后来的信息产生干扰,使大脑对后接触的信息印象不深,容易遗忘,看来孩子对学习新知产生遗忘是非常正常的。我们不能一味地抱怨孩子上课不用心,没有记住老师当堂讲的内容。孩子的遗忘是有规律的,德国著名的心理学家艾宾浩斯总结了遗忘规律并绘制成图,被称为“艾宾浩斯遗忘曲线”,请看图:
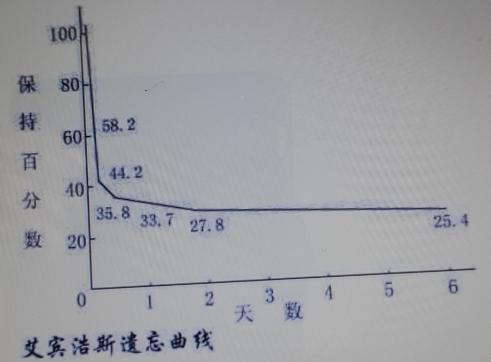
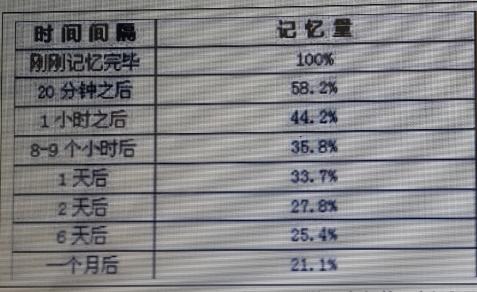
从上图我们可以看出:遗忘的速度是先快后慢,遗忘速度最快的区段是20分钟、1小时、24小时,分别遗忘42%、56%、66%;2—31天遗忘率稳定在72%—79%之间,过了这个区段因已遗忘了材料的72%以上,所以复习起来就“事倍功半”。我们在复习功课时,有时感觉碰到的好像是新知识似的,这就是因为复习的间隔太长了的缘故。所以不能认为隔几小时与隔几天复习是一回事,应及时复习,间隔一般不超过2天。及时复习,强化印象,这就是我们讲过新知后都要做一些相对应的练习题的目的所在。复习就是对大脑中的痕迹进行再刺激,及时复习就是在第一次痕迹未完全消失时,紧接着进行第二次,第三次重复刺激,重复刺激次数越多,痕迹越深;重复越及时,费时越少,费力越小,记忆效果越好。今后我们要有意识的运用这一规律,切莫以为什么时间复习都一样。如果我们的课程表一天安排两节数学课是最好的,第一节是新授课,老师带领学生一起探究新知,第二节引领学生进行集中复习,其实也就是我们平常所说的练习课。练习课的设计题目要有代表性,层次性、难易要适度。怎样设计练习课才会高效呢?下面以“长方体正方体表面积计算”为例加以说明。
设计原则:
我设计不同层次的练习,目的逐步加深学生对“长方体正方体表面积计算方法”的理解。
1、 基础练习
(1)长方体和正方体6个面的面积总和叫( )。
长方体的表面积公式是( ),正方体的表面积公式是( )。
(2)求下面图形的面积。
长
宽
高
表面积
长方体
5分米
4分米
3分米
正方体
6厘米
6厘米
6厘米
【目的:通过练习,加深学生对长方体正方体表面积公式的理解。】
2、 深化练习:
(1)一个正方体的棱长总和是60厘米,它的棱长是( )厘米,表面积是( )c㎡。
(2)一个正方体的底面积是4平方分米,它的表面积是( )平方分米。
(3)一个长方体长是12米,宽是7米,高是3米,它的占地面积最大是( )平方米,最小是( )平方米。
【目的:这里将“底面积、表面积、占地面积”等情况都展现出来,让学生进一步明确物体的占地面积,底面积是相对的,都是相对“地面”来说的。只有物体的表面积是一定的,它是指一个物体6个面的面积和。
3.提高练习:选择题
(1)求学校教学楼的占地面积,就是求教学楼( )。
A、底面积 B、侧面积 C、表面积
(2)一个长方体的长、宽、高都扩大2倍,
表面积扩大( )。
A、2 B、4 C、6
(3)讨论:比较两个图形的表面积( )
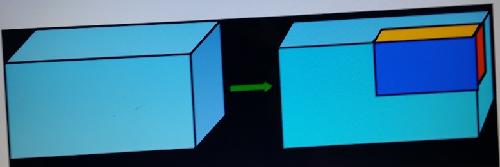
A.甲的表面积大
B.乙的表面积
C.它们的表面积相等
D.可能甲的表面积大,也可能乙的表面积大
【目的:让学生对物体表面积的理解得到进一步升华。】
3.拓展练习:
《新华字典》的长10cm、宽8cm、高3cm。
1、如果用纸把2本《新华字典》包起来,
有几种包法?那种包法最节省纸?
2、最少需要多少平方厘米的纸?

【目的:培养学生从不同的角度思考问题,训练学生思维的有序性和灵活性。】