我的众享收获——几何篇
几何天生就是我的弱项,为了弥补这一缺憾,众享可是帮了我不少大忙。说起几何,那可是令许多人闻风丧胆的,经过众享细细讲解,在老师的循循善诱下,原来几何是如此的简单——只不过是一个数形结合罢了。我有众享,任难题来袭,我自岿然不动!
一、 知识点梳理
(一) 勾股定理
文字语言:直角三角形两条直角边的平方和等于斜边的平方。
符号语言:若一个直角三角形的两直角边边长分别为a、b,斜边长为c,则满足a²+b²=c²
做题书写格式:在RT△ABC中,∠C=90°
由勾股定理得:
c²=a²+b²=3²+4²=25
∵c>0
∴c=5
注意:勾股定理只适用于直角三角形中
(二) 勾股定理的逆定理
文字语言:如果三角形两条直角边的平方和等于第三边斜边的平方,那么这个三角形就是直角三角形
符号语言:如果三角形的三边长a,b,c满足a²+b²=c²,那么这个三角形为直角三角形
做题书写格式:∵a²+b²=3²+4²=25
C²=5²=25
∴a²+b²=c²
∴△ABC为直角三角形
注意:最长边(直角所对的边)为斜边
(三) 勾股定理及逆定理的应用
① 画直角
② 在数轴上表示无理数
(四) 平行四边形及其性质
定义:两组对边分别平行的四边形是平行四边形
性质1:平行四边形的对边相等
做题格式:∵四边形ABCD为平行四边形
∴AB=CD,BC=AD
性质2:平行四边形的对角相等
做题格式:∵四边形ABCD为平行四边形
∴∠A=∠C, ∠B=∠D
性质3:平行四边形的对角线互相平分
做题格式:∵四边形ABCD为平行四边形
∴AO=BO,CO=DO
注意:只求出需要的条件即可,不必重复
(五) 平行四边形的判定
判定1:两组对边分别平行的四边形是平行四边形(定义)
做题格式:在四边形ABCD中,AB∥CD,BC∥AD
∴四边形ABCD是平行四边形
判定2:两组对边分别相等的四边形是平行四边形
做题格式:在四边形ABCD中,AB=CD,BC=AD
∴四边形ABCD是平行四边形
判定3:两组对角分别相等的四边形是平行四边形
做题格式:在四边形ABCD中,∠A=∠C, ∠B=∠D
∴四边形ABCD是平行四边形
判定4:对角线互相平分的四边形是平行四边形
做题格式:在四边形ABCD中,AO=BO,CO=DO
∴四边形ABCD是平行四边形
判定5:一组对边平行且相等的四边形是平行四边形
做题格式:在四边形ABCD中,AB=CD,AB∥CD
∴四边形ABCD是平行四边形
(六) 三角形的中位线定理
定义; 三角形的中位线平行于第三边,并且等于第三边的一半
做题格式:在△ABC中
∵M为AB中点,N为AC中点
∴MN为△ABC的中位线
∴MN=1/2BC,MN∥BC
(七)矩形的定义及性质
定义:有一个角是直角的平行四边形是矩形
性质:具有平行四边形的所有性质
特殊性质1:矩形的4个内角都是直角
做题格式:∵平行四边形ABCD为矩形
∴∠A=∠B=∠C=∠D=90°
特殊性质2:矩形的对角线相等
做题格式:∵平行四边形ABCD为矩形
∴AC=BD
(七) 直角三角形斜边中线定理
定义:直角三角形斜边上的中线等于斜边的一半
做题格式:在RT△ABC中,∠C =90°,AD=BD=1/2AB
∴CD=AD=BD=1/2AB
逆命题:成立,可用来判定直角三角形
注意:直角三角形三个中点所构成的三角形,面积是原直角三角形的四分之一,周长为其一半
(八) 矩形的判定
判定1:有一个角是直角的平行四边形是矩形
做题格式:∵四边形ABCD为平行四边形,且∠A=90°
∴平行四边形ABCD为矩形
判定2:对角线相等的平行四边形是矩形
做题格式:∵四边形ABCD为平行四边形,且AC=BD
∴平行四边形ABCD为矩形
判定3:有三个角是直角的四边形是矩形
做题格式:在四边形ABCD中,∵∠A=∠B=∠C=90°
∴四边形ABCD为矩形
注意:矩形是特殊的平行四边形,拥有平行四边形的所有性质,但是不可以用平行四边形的判定来判断矩形!
(九) 菱形的定义及性质
定义:有一组邻边相等的平行四边形是菱形
特殊性质1:菱形的四条边都相等
做题格式:∵平行四边形ABCD为菱形
∴AB=BC=CD=AD
特殊性质2:菱形的对角线互相垂直,且每一条对角线平分
一组对角
做题格式:∵平行四边形ABCD为菱形
∴AC⊥BD,∠ADB=∠CDB=∠ADB=∠CBD,∠CAD=∠CAB=∠DCA=∠BCA
(十) 菱形的判定
判定1:有一组邻边相等的平行四边形是菱形
做题格式:在平行四边形ABCD中,∵AB=BC
∴平行四边形ABCD为菱形
判定2:对角线互相垂直的平行四边形是菱形
做题格式:在平行四边形ABCD中,∵AC⊥BD
∴平行四边形ABCD为菱形
判定3:四条边都相等的四边形是菱形
做题格式:在四边形ABCD中,∵AB=BC=CD=AD
∴四边形ABCD为菱形
(十一)正方形
定义:正方形是具有四条相等的边和四个相等内角组合成的多边形
性质:边(四边相等、对边平行、邻边垂直)
角(四个角均为直角)
对角线(互相垂直平分且相等,每一条对角线平分一组对角)
即:具有平行四边形、矩形、菱形的一切性质(正方形是特殊的平行四边形,既是矩形,又是菱形)
判定1:一组邻边相等的矩形是正方形
做题格式:在矩形ABCD中,∵AB=BC
∴矩形ABCD为正方形
判定2:有一个内角是直角的菱形是正方形
做题格式:在菱形ABCD在,∵∠A=90°
∴菱形ABCD为正方形
判定3:对角线相等的菱形是正方形
做题格式:在菱形ABCD中,∵AC=BD
∴菱形ABCD为正方形
判定4:对角线互相垂直的矩形是正方形
做题格式:在矩形ABCD中,AC⊥BD
∴矩形ABCD为正方形
我的话:正方形的判定即只要证明出一个平行四边形既是矩形,又是菱形即可。做题如果不按格式可能会被扣分。
二、 注意
1. 不要循环论证(利用一个已经推出来结论的去证明另一个结论,再反之去证明已经推出来的结论)
2. 注意审题(不要放过任何的条件,哪怕是“AC、BD交于点O”,也有可能会推出对顶角)
3. 全等方面(如果一道题用一次全等没有思路,那就用二次全等,只要思路正确就不会扣分)
三、 关于几何的简便方法
1、 在一个直角三角形中,如果有一个角=30°,那么较短的直角边(长度):较长的直角边(长度):斜边(长度)=1:根号3:2
2、 在等腰直角三角形中,腰长:腰长:底边长=1:1:根号2
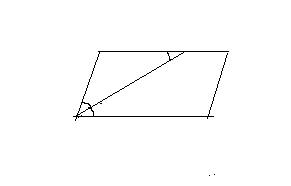
3、 出现平行四边形和角平分线,一般可以推出等腰三角形(图中标出的角都是相等的)
4、 遇到等腰三角形和底边的中线时,考虑三线合一
5、 遇到直角三角形斜边的中点,考虑直角三角形斜边上的中线等于斜边的一半
6、 遇到三角形任意一边的中线,考虑倍长中线
7、 多个中点,考虑中位线
8、 不规则四边形的面积计算方法
(1) 补齐,使其成为一个规则图形
(2) 在内部截成几个规则图形
(3) 若对角线垂直,面积等于对角线乘积的一半
9、 出现多个等边三角形,考虑全等或构造全等
我的话:这些简便方法都是在做题中探索出来的,填空选择可以节省不少时间,但是应用题千万不要跳步!
附;四边形拔高课
http://v.xxt.cn/course/1157.html
着重讲解中点,几何计算与证明,类比探究,四边形与动点、存在性问题结合等知识,前两块侧重模块化讲解,常应用于中考大题,后两块是中考难点题型的提前训练。