猴子和水果
过节了,家家户户都买了年货,猴子家也不例外,猴妈妈买了孩子们最爱吃的苹果拿回家里。
“孩子们,都快来啊,看妈妈买什么回来了。”猴妈妈一到家就喊了起来。大猴和小猴忙跑出来,看着苹果直流口水。
“孩子们,要想吃苹果,按照惯例,需要解决一个问题。今天的问题和苹果有关。”猴妈妈这时候倒是不紧不慢起来,“请听题:把苹果和梨混放在一个筐里,小熊把这筐水果分成了若干堆,后来发现无论怎么分,总能从这若干堆里找到两堆,把这两堆水果合并在一起后,苹果和梨的个数是偶数,那么小熊至少把这些水果分成了几堆?”
大猴和小猴都很聪明,但是以前妈妈没有问过这样类似的问题,他们两个都抓耳挠腮分析了起来。大猴说:“题中要求把其中两堆合并在一起后,苹果和梨的个数一定是偶数,那么这两堆水果中,苹果和梨的奇偶性必须相同。”小猴说:“对于每一堆苹果和梨,奇偶可能性有4种:(奇,奇),(奇,偶),(偶,奇),(偶,偶),那究竟该咋分呢?”大猴和小猴你看着我,我看着你不知道应该怎样往下思考了。
“孩子们,你们分析得都很有道理,只差一步就能成功了。今天我给你们讲一个数学原理,只要掌握了很快就能解决这个问题。”猴妈妈高兴的说到。
“桌上有三个苹果,要把这三个苹果放到两个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面至少放两个苹果。这一现象就是我要给你们说的‘抽屉原理’。
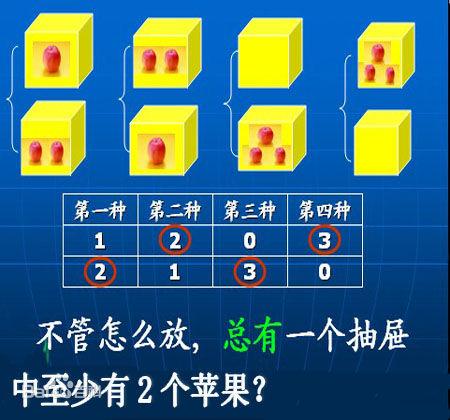
用数学的语言可以这样描述抽屉原理:‘如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1或多于n+1个元素放到n个集合中去,其中必定至少有一个集合里有两个元素。’ 抽屉原理有时也被称为鸽巢原理(‘如果有五个鸽子笼,养鸽人养了6只鸽子,那么当鸽子飞回笼中后,至少有一个笼子中装有至少2只鸽子’)。它是组合数学中一个重要的原理。怎么样,听懂了吗?”猴妈妈终于把“抽屉原理”给她的孩子们讲完了。
“怎样证明呢?”猴子们还觉得意犹未尽。
“这个可以用反证法。”猴妈妈好像早有准备,“原理: 把多于n个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。证明(反证法):如果每个抽屉至多只能放进一个物体,那么物体的总数至多是n,而不是题设的n+k(k≥1),故不可能。”
“有意思。那具体到您出的题上,可不可以用‘抽屉原理’这样理解:既然对于每一堆苹果和梨,奇偶可能性有4种,那么小熊至少要把这些水果分成4+1=5堆才能满足题目的要求。”小猴先人一步把问题解决了。
猴妈妈满意的点了点头,先给小猴发了个苹果。