画线段图解题例谈
——解决问题方法之一
线段图是一种重要的数形结合的数学思想方法。画线段图是指用一条或几条线段表示题中的数量关系,使数量关系直观、清晰,从而使数学问题得以顺利解决的一种解题策略。随着学生年级的升高、只是难度的加深,有些问题借助画线段图的方法做起来就显得简单多了。在我们三年级有这样几类问题可以使用这种方法。
1、运用画线段图解决植树问题。
例:工人叔叔在一条50米长的小路一旁植树,起点和终点各栽一棵,一共栽了6棵树,每相邻两棵树之间距离相等。相邻两棵树之间相距多少米?
分析:画线段图理解题意:

起点和终点哥在一棵树,一共栽了6棵树,6棵树之间的距离是50米,有5个间隔,一个间隔的长度就是相邻两棵树之间的距离。
解答:6-1=5(个)
50÷5=10(米)
答:相邻两棵树之间相距10米。
解决这类问题,可先用植树的棵数减1求出间隔数,再用总长度除以间隔数求出相邻两棵树之间的距离。







2、运用画线段图法求除数。
例:两个整数相除没有余数,商是8,被除数、除数、商的和是71。求除数是多少?
分析:这道题可以转化成和倍问题来计算。根据题意可知,被除数与除数的和71-8=63,商是8,也就是被除数是除数的8倍,画线段图如下:
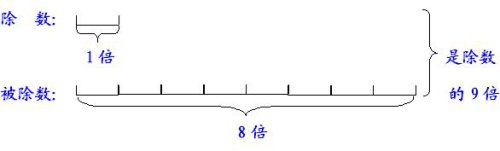
因此除数是63÷9=7
解答:71-8=63 8+1=9 63÷9=7
答:除数是7。
两个整数相除没有余数,商是几,被除数就是除数的几倍。










3、运用画线段图解决和差问题。
例:实验小学三年级和四年级共为灾区捐款540元,四年级比三年级多捐60元,三年级和四年级各捐多少元?
分析:通过画线段图来理清题中的数量关系。
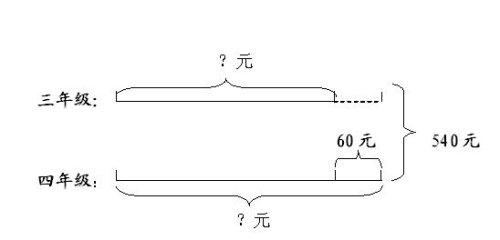
从线段图中可以看出,如果三年级捐的钱数增加60元,也就是在540元的基础上增加60元,所得的和正好是四年级捐款的2倍,可以求出四年级捐的钱数,然后再求出三年级捐的钱数。
解答:
四年级: (540+60)÷2 三年级:300-60=240(元)
=600÷2
=300(元)
答:三年级捐款240元,四年级捐款300元。
和差问题的解题方法是:大数=(和+差)÷2 小数=(和-差)÷2;列综合算式时一定要用小括号。









4、运用画线段图解决分数比较大小问题。
例:判断:一袋糖块的2/4比另一袋糖块的1/4多。 ( )
分析:虽然2/4>1/4,但题中不是比较两个分数的大小,二是比较两袋糖的2/4和1/4分别所代表的具体数量。
(1)如果两袋糖块的数量相等,则有:
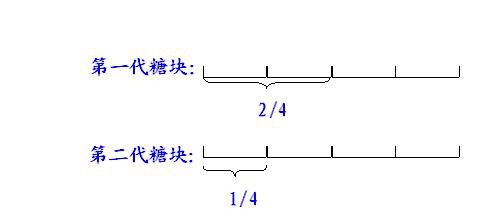
2/4>1/4,第一袋糖块的2/4多于第二袋糖块的1/4。
(2)如果两袋糖块的数量不相等,则有可能:
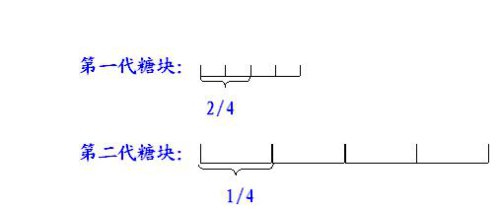
第二袋糖块的1/4反而多于第一袋糖块的2/4.
因此,题中的说法是错误的。
在两个整体所代表的数量不确定时,不能比较它们几分之几的大小。
画线段法解决问题贯穿于整个小学数学教学中,我们要善于利用各种教学时机,实时渗透引导,使学生逐步掌握“画图策略”的技能,逐渐形成良好的思维习惯,增进学生理解力、思考力、以及创造力的提高。