回溯法求图的m着色问题
?
?
?
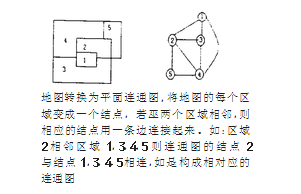
问题描述:给定无向图G和m种不同的颜色,用这些颜色为图G的各个点着色,每个顶点着一种颜色。是否有一种着色发使G中的每条边的两个顶点着不同种颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中的每一条边连接的两个顶点着不同种颜色,则称这个数m为该图的色数。图的色数m的问题称为图的m可着色优化问题。
?
?
?解题思路:有序地从顶点1着1号颜色开始,然后再试着顶点2的第几号颜色,如果顶点2也满足条件,那么继续着顶点3的颜色,如果此时顶点3没有可着的颜色,说明目前为止的尝试是无效的(不可能得到最终的解),那么此时应该回溯的上一顶点(即顶点2),将上一顶点着的颜色该着另一种符合要求的颜色..........如此尝试性地搜索加回溯,最后得到符合要求的解。
?
?
package 算法实验;/** * 图的m着色类 *回溯法求图的m着色问题 */public class mColoring {//定义变量和数组static int m,n;//m为颜色种数,n表示n个区域static int []x;//x[k]表示第k号区域的第x[k]号颜色static int [][]a;//用来存储图的邻接矩阵 /** * 如何着色的方法 */ public void coloring(){ x[1]=0;//每号区域从0号颜色开始 int k=1;//从1号区域开始 while(k>0){ x[k]=x[k]+1; while((x[k]<=m)&&!(restrain(k)))//约束条件判断 x[k]+=1; if(x[k]<=m) if(k==n){ //输出各个区域着的颜色 for(int i=1;i<=n;i++) System.out.println(+i+"号区域着"+x[i]+"号颜色;"); System.out.println(); } else { k++; x[k]=0; } else k--;//回溯 } } /** * 约束条件的判断方法 * @param k * @return */ public boolean restrain(int k){ for(int j=1;j<=k;j++) if((a[k][j]==1)&&(x[j]==x[k]))//相邻区域不能着同种颜色 return false; return true; } /** * 程序入口,主函数 * @param args */ public static void main(String[] args){ m=4;n=5;//给m,n赋初始值 x = new int[n+1];//定义数组长度 //二维数组用来存储图的邻接矩阵 a=new int[][]{{0,0,0,0,0,0},//0表示两号区域之间不相邻{0,0,1,1,1,0},//1表示两号区域之间相邻{0,1,0,1,1,1},{0,1,1,0,1,0},{0,1,1,1,0,1},{0,0,1,0,1,0}}; mColoring mc = new mColoring();//实例化对象 System.out.println("各个点着的颜色是:"); mc.coloring();//调用着色方法 } }?运行结果:
?
1号区域着4号颜色;
2号区域着3号颜色;
3号区域着1号颜色;
4号区域着2号颜色;
5号区域着1号颜色;
?
1号区域着4号颜色;
2号区域着3号颜色;
3号区域着1号颜色;
4号区域着2号颜色;
5号区域着4号颜色;
?
1号区域着4号颜色;
2号区域着3号颜色;
3号区域着2号颜色;
4号区域着1号颜色;
5号区域着2号颜色;
?
1号区域着4号颜色;
2号区域着3号颜色;
3号区域着2号颜色;
4号区域着1号颜色;
5号区域着4号颜色;