CF-209-div-2 (CF-359A-D)
CF-359A. Table
题目链接：
http://codeforces.com/problemset/problem/359/A
题目意思：
给一个矩阵n*m，1为好格子，0为坏格子。四个角落没有好格子，每次可以选择一个好格子和四个角落任意一个格子，使得这两个格子组成的矩形全部选中，求最少需要几次能把整个矩阵全部选中。一个格子可以选多次。
解题思路：
简单贪心题。如果好格子在边界则只需两次，否则需要四次（每个角落个字操作一次）。
代码：
#include<iostream>#include<cmath>#include<cstdio>#include<sstream>#include<cstdlib>#include<string>#include<string.h>#include<cstring>#include<algorithm>#include<vector>#include<map>#include<set>#include<stack>#include<list>#include<queue>#include<ctime>#include<bitset>#define eps 1e-6#define INF 0x3f3f3f3f#define PI acos(-1.0)#define ll __int64#define LL long long#define lson l,m,(rt<<1)#define rson m+1,r,(rt<<1)|1#define M 1000000007#pragma comment(linker, "/STACK:1024000000,1024000000")using namespace std;#define Maxn 51000int main(){ //freopen("in.txt","r",stdin); //freopen("out.txt","w",stdout); int n,k; while(~scanf("%d%d",&n,&k)) { int p,q; if(k) //k不等于0，构造第一项1,k+1其余的为2~2*n之间不为k+1的，且a[2*i-1]>a[2*i]即可 { printf("%d %d ",1,k+1); p=2,q=2*n; } else { printf("%d %d ",2,1); //如果k=0,为了统一使得k=1,p=3,q=2*n k=1; p=3,q=2*n; } for(int i=1;i<n;i++) //其余的一个大，一个小，用两个指针构造即可 { if(p==k+1) //排除k+1的情况 p++; if(q==k+1) q--; printf("%d %d ",q,p); p++; q--; } putchar('\n'); } return 0;}题目链接：
http://codeforces.com/problemset/problem/359/C
题目意思：
给一个质数X，和n个数a1<=a2<=...<=an.求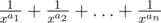
通分得到分母t=x^(a1+a2+...+an),分子为s,求s,t的最大公约数。（ai<=10^9,n<=3*10^5).
解题思路：
快速幂+数学。
由于数据范围很大，硬搞肯定是不行的。分析发现，分母为x^sum,记sum=a1+a2+...+an，分子的各项为x^(sum-ai).显然分子中每项一定可以提出一个min(a^(sum-ai))出来，此时如果min(a^(sum-ai))有x的倍数个，还需向前进位。
代码：
#include<iostream>#include<cmath>#include<cstdio>#include<sstream>#include<cstdlib>#include<string>#include<string.h>#include<cstring>#include<algorithm>#include<vector>#include<map>#include<set>#include<stack>#include<list>#include<queue>#include<ctime>#include<bitset>#define eps 1e-6#define INF 0x3f3f3f3f#define PI acos(-1.0)#define ll __int64#define LL long long#define lson l,m,(rt<<1)#define rson m+1,r,(rt<<1)|1#define M 1000000007#pragma comment(linker, "/STACK:1024000000,1024000000")using namespace std;#define Maxn 400000int le[Maxn],ri[Maxn],save[Maxn],n;int ans[Maxn];vector<int>myv;int main(){ //freopen("in.txt","r",stdin); //freopen("out.txt","w",stdout); while(~scanf("%d",&n)) { for(int i=1;i<=n;i++) { scanf("%d",&save[i]); ans[i]=0; le[i]=ri[i]=i; } myv.clear(); for(int i=2;i<=n;i++) { int tt=i-1; while(save[tt]%save[i]==0&&tt>=1) //如果能整除，它包含的区间也一定能被save[i]整除 tt=le[tt]-1; le[i]=le[tt+1]; } for(int i=n-1;i>=1;i--) { int tt=i+1; while(save[tt]%save[i]==0&&tt<=n) { tt=ri[tt]+1; } ri[i]=ri[tt-1]; } for(int i=1;i<=n;i++) //统计区间 { int temp=le[i],len=ri[i]-le[i]; if(len>ans[temp]) ans[temp]=len; } int Max=0; for(int i=1;i<=n;i++) //找到最大的 { if(ans[i]>Max) { Max=ans[i]; myv.clear(); myv.push_back(i); } else if(ans[i]==Max) myv.push_back(i); } /*for(int i=1;i<=n;i++) { if(ans[i]==Max) myv.push_back(i); }*/ printf("%d %d\n",myv.size(),Max); for(int i=0;i<myv.size();i++) printf("%d ",myv[i]); putchar('\n'); } return 0;}