每日ACM学习以及小水题 2013年11月3日
说明
为了向大神看齐,遂响应号召,每天刷一下POJ上面的水题,每天学习一点ACM,做一点ACM题目。
我相信积少成多,更相信,开头是艰难的,但是一旦走进去,就会别有一番感受,速度也会加快吧。
so ,today is the first day .
POJ 1003 (传送门:http://poj.org/problem?id=1003)
题目描述:
Description
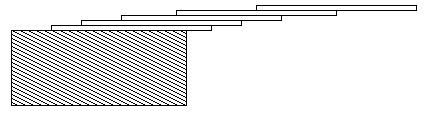
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
Input
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.Output
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.找所有的(n, k), 满足: 1+2+..+(n-1)=(n+1)+(n+2)…+k 。输出按k排序的前6个。
第二题:数论相关的题目【分析过程】整理得: n(n-1)=(k-n)(n+k+1),化简得: k2+k-2n2=0, 即n2=k(k+1)/2,由于k和k+1互素, 因此
----要么k是完全平方数
----要么k/2是完全平方数
分别设k=m2和2m2, 枚举m
代码如下:
【未完待续】..............