算法入门系列2-DP入门之DAG上的DP
算法入门系列二--DP入门之DAG上的DP引言：DAG：有向无环图。DAG是学习动态规划的基础，很多问题都可以直接转化
算法入门系列二--DP入门之DAG上的DP
引言：
DAG：有向无环图。
DAG是学习动态规划的基础，很多问题都可以直接转化为DAG上的最长路、最短路或路径计数问题。
两个经典的DAG模型，嵌套矩形和硬币问题，今天先写第一个嵌套矩形问题。
一、嵌套矩形第一个DAG模型：矩形嵌套问题描述有n个矩形，每个矩形可以用a,b来描述，表示长和宽。
矩形X(a,b)可以嵌套在矩形Y(c,d)中当且仅当a<c,b<d或者b<c,a<d（相当于旋转X90度）。
例如（1,5）可以嵌套在（6,2）内，但不能嵌套在（3,4）中。
你的任务是选出尽可能多的矩形排成一行，使得除最后一个外，每一个矩形都可以嵌套在下一个矩形内。
【分析】矩形间的“可嵌套”关系是一个典型的二元关系，二元关系可以用图来建模。如果矩形X可以嵌套在Y中，则就从X到Y连一条有向边。这个图是无环的，因为一个矩形无法直接或或间接的嵌套在自己的内部。也即是说这是以一个DAG。因此，我们就是在求DAG上的最长路径。
【问题】这个是一个没有确定的路径起点和终点（可以把任意的矩形放在任何位置）的DAG问题。如何求解，仿照上次的数字三角形（数塔）问题的求解，可以设d（i）表示从节点i出发的最长路的长度，如何写出状态转移方程呢？第一步只能走到他的相邻的节点，因此：
d（i）= max { d（j）+1 | i, j ∈E }其中，E为边集。最终答案是所有的d（i）中的最大值。因此可以用递推或者记忆化搜索计算。
二、解决步骤
第一步，建图。假如用邻接矩阵将矩形间的关系保存在矩阵G中。
第二步，编写记忆化搜索程序（调用前先初始化数组为0）。
第三步，按字典序输出最佳的方案三、实例实践假如有这样的五个矩形：输入的边长分别是：
矩形宽矩形长3546237466其DAG表示如下：
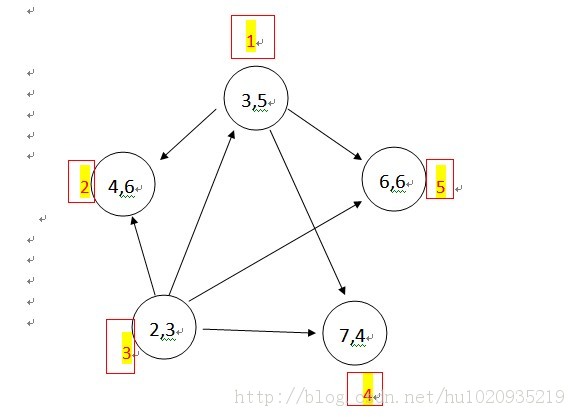由图可知，最长路有3--1--2 和 3--1--4
按字典序之后只有 3--1--2具体的代码如下：（c语言实现DAG矩形嵌套问题）
附录：代码
未完待续。。。。下一个---DAG之硬币问题（固定终点的最短路问题）。
