※数据结构※→☆非线性结构(tree)☆============哈夫曼树 顺序存储结构(tree Huffman sequence)(二十二)
哈夫曼树 (Huffman Tree)
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree)。
哈夫曼树(霍夫曼树)又称为最优树.
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
哈夫曼树构造过程
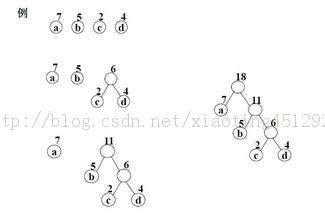
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
树的四种遍历
1.先序遍历 (仅二叉树)
指先访问根,然后访问孩子的遍历方式
2.中序遍历(仅二叉树)
指先访问左(右)孩子,然后访问根,最后访问右(左)孩子的遍历方式
3.后序遍历(仅二叉树)
指先访问孩子,然后访问根的遍历方式
4.层次遍历
一层一层的访问,所以一般用广度优先遍历。
======================================================================================================
树结点 顺序存储结构(tree node sequence)
结点:
包括一个数据元素及若干个指向其它子树的分支;例如,A,B,C,D等。在数据结构的图形表示中,对于数据集合中的每一个数据元素用中间标有元素值的方框表示,一般称之为数据结点,简称结点。
在C语言中,链表中每一个元素称为“结点”,每个结点都应包括两个部分:一为用户需要用的实际数据;二为下一个结点的地址,即指针域和数据域。
数据结构中的每一个数据结点对应于一个储存单元,这种储存单元称为储存结点,也可简称结点
树结点(树节点):
树节点相关术语:
节点的度:一个节点含有的子树的个数称为该节点的度;叶节点或终端节点:度为0的节点称为叶节点;非终端节点或分支节点:度不为0的节点;双亲节点或父节点:若一个结点含有子节点,则这个节点称为其子节点的父节点;孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;兄弟节点:具有相同父节点的节点互称为兄弟节点;节点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;堂兄弟节点:双亲在同一层的节点互为堂兄弟;节点的祖先:从根到该节点所经分支上的所有节点;子孙:以某节点为根的子树中任一节点都称为该节点的子孙。根据树结点的相关定义,采用“双亲孩子表示法”。其属性如下:
2.孩子表示法
1.多重链表:每个结点有多个指针域,分别指向其子树的根
1)结点同构:结点的指针个数相等,为树的度k,这样n个结点度为k的树必有n(k-1)+1个空链域.
2)结点不同构:结点指针个数不等,为该结点的度d
2.孩子链表:每个结点的孩子结点用单链表存储,再用含n个元素的结构数组指向每个孩子链表
3.双亲孩子表示法
1.双亲表示法,PARENT(T,x)可以在常量时间内完成,但是求结点的孩子时需要遍历整个结构。
2.孩子链表表示法,适于那些涉及孩子的操作,却不适于PARENT(T,x)操作。
3.将双亲表示法和孩子链表表示法合在一起,可以发挥以上两种存储结构的优势,称为带双亲的孩子链表表示法
4.双亲孩子兄弟表示法 (二叉树专用)
又称为二叉树表示法,以二叉链表作为树的存储结构。
顺序存储结构
在计算机中用一组地址连续的存储单元依次存储线性表的各个数据元素,称作线性表的顺序存储结构.
顺序存储结构是存储结构类型中的一种,该结构是把逻辑上相邻的节点存储在物理位置上相邻的存储单元中,结点之间的逻辑关系由存储单元的邻接关系来体现。由此得到的存储结构为顺序存储结构,通常顺序存储结构是借助于计算机程序设计语言(例如c/c++)的数组来描述的。
顺序存储结构的主要优点是节省存储空间,因为分配给数据的存储单元全用存放结点的数据(不考虑c/c++语言中数组需指定大小的情况),结点之间的逻辑关系没有占用额外的存储空间。采用这种方法时,可实现对结点的随机存取,即每一个结点对应一个序号,由该序号可以直接计算出来结点的存储地址。但顺序存储方法的主要缺点是不便于修改,对结点的插入、删除运算时,可能要移动一系列的结点。
优点:
随机存取表中元素。缺点:插入和删除操作需要移动元素。
本代码默认list可以容纳的item数目为100个,用户可以自行设置item数目。当list饱和时,由于Tree是非线性结构,动态扩展内存相当麻烦。因此示例中的Demo及代码将不会动态扩展内存。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
以后的笔记潇汀会尽量详细讲解一些相关知识的,希望大家继续关注我的博客。
本节笔记到这里就结束了。
潇汀一有时间就会把自己的学习心得,觉得比较好的知识点写出来和大家一起分享。
编程开发的路很长很长,非常希望能和大家一起交流,共同学习,共同进步。
如果文章中有什么疏漏的地方,也请大家指正。也希望大家可以多留言来和我探讨编程相关的问题。
最后,谢谢你们一直的支持~~~
C++完整个代码示例(代码在VS2005下测试可运行)
AL_TreeNodeBinSeq.h
树的四种遍历
1.先序遍历 (仅二叉树)
指先访问根,然后访问孩子的遍历方式
2.中序遍历(仅二叉树)
指先访问左(右)孩子,然后访问根,最后访问右(左)孩子的遍历方式
3.后序遍历(仅二叉树)
指先访问孩子,然后访问根的遍历方式
4.层次遍历
一层一层的访问,所以一般用广度优先遍历。
======================================================================================================
树结点 顺序存储结构(tree node sequence)
结点:
包括一个数据元素及若干个指向其它子树的分支;例如,A,B,C,D等。在数据结构的图形表示中,对于数据集合中的每一个数据元素用中间标有元素值的方框表示,一般称之为数据结点,简称结点。
在C语言中,链表中每一个元素称为“结点”,每个结点都应包括两个部分:一为用户需要用的实际数据;二为下一个结点的地址,即指针域和数据域。
数据结构中的每一个数据结点对应于一个储存单元,这种储存单元称为储存结点,也可简称结点
树结点(树节点):
树节点相关术语:
节点的度:一个节点含有的子树的个数称为该节点的度;叶节点或终端节点:度为0的节点称为叶节点;非终端节点或分支节点:度不为0的节点;双亲节点或父节点:若一个结点含有子节点,则这个节点称为其子节点的父节点;孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;兄弟节点:具有相同父节点的节点互称为兄弟节点;节点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;堂兄弟节点:双亲在同一层的节点互为堂兄弟;节点的祖先:从根到该节点所经分支上的所有节点;子孙:以某节点为根的子树中任一节点都称为该节点的子孙。根据树结点的相关定义,采用“双亲孩子表示法”。其属性如下:
2.孩子表示法
1.多重链表:每个结点有多个指针域,分别指向其子树的根
1)结点同构:结点的指针个数相等,为树的度k,这样n个结点度为k的树必有n(k-1)+1个空链域.
2)结点不同构:结点指针个数不等,为该结点的度d
2.孩子链表:每个结点的孩子结点用单链表存储,再用含n个元素的结构数组指向每个孩子链表
3.双亲孩子表示法
1.双亲表示法,PARENT(T,x)可以在常量时间内完成,但是求结点的孩子时需要遍历整个结构。
2.孩子链表表示法,适于那些涉及孩子的操作,却不适于PARENT(T,x)操作。
3.将双亲表示法和孩子链表表示法合在一起,可以发挥以上两种存储结构的优势,称为带双亲的孩子链表表示法
4.双亲孩子兄弟表示法 (二叉树专用)
又称为二叉树表示法,以二叉链表作为树的存储结构。
顺序存储结构
在计算机中用一组地址连续的存储单元依次存储线性表的各个数据元素,称作线性表的顺序存储结构.
顺序存储结构是存储结构类型中的一种,该结构是把逻辑上相邻的节点存储在物理位置上相邻的存储单元中,结点之间的逻辑关系由存储单元的邻接关系来体现。由此得到的存储结构为顺序存储结构,通常顺序存储结构是借助于计算机程序设计语言(例如c/c++)的数组来描述的。
顺序存储结构的主要优点是节省存储空间,因为分配给数据的存储单元全用存放结点的数据(不考虑c/c++语言中数组需指定大小的情况),结点之间的逻辑关系没有占用额外的存储空间。采用这种方法时,可实现对结点的随机存取,即每一个结点对应一个序号,由该序号可以直接计算出来结点的存储地址。但顺序存储方法的主要缺点是不便于修改,对结点的插入、删除运算时,可能要移动一系列的结点。
优点:
随机存取表中元素。缺点:插入和删除操作需要移动元素。
本代码默认list可以容纳的item数目为100个,用户可以自行设置item数目。当list饱和时,由于Tree是非线性结构,动态扩展内存相当麻烦。因此示例中的Demo及代码将不会动态扩展内存。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
以后的笔记潇汀会尽量详细讲解一些相关知识的,希望大家继续关注我的博客。
本节笔记到这里就结束了。
潇汀一有时间就会把自己的学习心得,觉得比较好的知识点写出来和大家一起分享。
编程开发的路很长很长,非常希望能和大家一起交流,共同学习,共同进步。
如果文章中有什么疏漏的地方,也请大家指正。也希望大家可以多留言来和我探讨编程相关的问题。
最后,谢谢你们一直的支持~~~
C++完整个代码示例(代码在VS2005下测试可运行)
AL_TreeNodeBinSeq.h#ifdef TEST_AL_TREEHUFFMANSEQAL_TreeHuffmanSeq<DWORD> cTreeBinSeq(100);BOOL bEmpty = cTreeBinSeq.IsEmpty();std::cout<<bEmpty<<std::endl;const AL_TreeNodeBinSeq<DWORD>* pConstRootNode = cTreeBinSeq.GetRootNode();AL_TreeNodeBinSeq<DWORD>* pRootNode = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstRootNode);std::cout<<pRootNode<<std::endl;DWORD dwDegree = cTreeBinSeq.GetDegree();std::cout<<dwDegree<<std::endl;DWORD dwHeight = cTreeBinSeq.GetHeight();std::cout<<dwHeight<<std::endl;DWORD dwNodesNum = cTreeBinSeq.GetNodesNum();std::cout<<dwNodesNum<<std::endl;DWORD dwWeight = 0x01;cTreeBinSeq.InsertRoot(0, dwWeight);pConstRootNode = cTreeBinSeq.GetRootNode();pRootNode = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstRootNode);std::cout<<pRootNode<<std::endl;dwWeight += 2;cTreeBinSeq.InsertLeftAtNode(pRootNode, 10, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode = cTreeBinSeq.GetChildNodeLeftAtNode(pRootNode);AL_TreeNodeBinSeq<DWORD>* pTreeNode = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode);std::cout<<pTreeNode<<std::endl;dwWeight += 2;cTreeBinSeq.InsertLeftAtNode(pTreeNode, 20, dwWeight);dwWeight += 2;cTreeBinSeq.InsertRightAtNode(pTreeNode, 21, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode20 = cTreeBinSeq.GetChildNodeLeftAtNode(pTreeNode);AL_TreeNodeBinSeq<DWORD>* pTreeNode20 = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode20);std::cout<<pTreeNode<<std::endl;dwWeight += 2;cTreeBinSeq.InsertLeftAtNode(pTreeNode20, 30, dwWeight);dwWeight += 2;cTreeBinSeq.InsertRightAtNode(pTreeNode20, 31, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode31 = cTreeBinSeq.GetChildNodeRightAtNode(pConstTreeNode20);AL_TreeNodeBinSeq<DWORD>* pTreeNode31 = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode31);dwWeight += 2;cTreeBinSeq.InsertLeftAtNode(pTreeNode31, 40, dwWeight);dwWeight += 2;cTreeBinSeq.InsertRightAtNode(pTreeNode31, 41, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode30 = cTreeBinSeq.GetChildNodeLeftAtNode(pConstTreeNode20);AL_TreeNodeBinSeq<DWORD>* pTreeNode30 = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode30);dwWeight += 2;cTreeBinSeq.InsertRightAtNode(pTreeNode30, 999, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode999 = cTreeBinSeq.GetChildNodeRightAtNode(pConstTreeNode30);AL_TreeNodeBinSeq<DWORD>* pTreeNode999 = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode999);dwWeight += 2;cTreeBinSeq.InsertLeftAtNode(pTreeNode999, 888, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode41 = cTreeBinSeq.GetChildNodeRightAtNode(pConstTreeNode31);AL_TreeNodeBinSeq<DWORD>* pTreeNode41 = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode41);dwWeight += 2;cTreeBinSeq.InsertRightAtNode(pTreeNode41, 52, dwWeight);const AL_TreeNodeBinSeq<DWORD>* pConstTreeNode33 = cTreeBinSeq.GetChildNodeRightAtNode(pTreeNode20);AL_TreeNodeBinSeq<DWORD>* pTreeNode33 = const_cast<AL_TreeNodeBinSeq<DWORD>*>(pConstTreeNode33);if (NULL != pTreeNode) {std::cout<<pTreeNode->GetLevel()<<" "<<pTreeNode->GetData()<<" "<<pTreeNode->GetDegree()<<std::endl;std::cout<<pTreeNode->IsLeaf()<<" "<<pTreeNode->IsBranch()<<" "<<pTreeNode->IsParent(pTreeNode)<<" "<<pTreeNode->IsParent(pTreeNode33)<<std::endl;}if (NULL != pTreeNode20) {std::cout<<pTreeNode20->GetLevel()<<" "<<pTreeNode20->GetData()<<" "<<pTreeNode20->GetDegree()<<std::endl;std::cout<<pTreeNode20->IsLeaf()<<" "<<pTreeNode20->IsBranch()<<" "<<pTreeNode20->IsParent(pTreeNode)<<" "<<pTreeNode20->IsParent(pTreeNode33)<<std::endl;}if (NULL != pTreeNode33) {std::cout<<pTreeNode33->GetLevel()<<" "<<pTreeNode33->GetData()<<" "<<pTreeNode33->GetDegree()<<std::endl;std::cout<<pTreeNode33->IsLeaf()<<" "<<pTreeNode33->IsBranch()<<" "<<pTreeNode33->IsParent(pTreeNode)<<" "<<pTreeNode33->IsParent(pTreeNode33)<<std::endl;}const AL_TreeNodeBinSeq<DWORD>*pChild = NULL;pChild = cTreeBinSeq.GetChildNodeRightAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<" "<<pChild->GetData()<<" "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<" "<<pChild->IsBranch()<<" "<<pChild->IsParent(pTreeNode)<<" "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeBinSeq.GetChildNodeLeftAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<" "<<pChild->GetData()<<" "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<" "<<pChild->IsBranch()<<" "<<pChild->IsParent(pTreeNode)<<" "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeBinSeq.GetChildNodeLeftAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<" "<<pChild->GetData()<<" "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<" "<<pChild->IsBranch()<<" "<<pChild->IsParent(pTreeNode)<<" "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeBinSeq.GetChildNodeRightAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<" "<<pChild->GetData()<<" "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<" "<<pChild->IsBranch()<<" "<<pChild->IsParent(pTreeNode)<<" "<<pChild->IsParent(pTreeNode33)<<std::endl;}pChild = cTreeBinSeq.GetChildNodeRightAtNode(pTreeNode);if (NULL != pChild) {std::cout<<pChild->GetLevel()<<" "<<pChild->GetData()<<" "<<pChild->GetDegree()<<std::endl;std::cout<<pChild->IsLeaf()<<" "<<pChild->IsBranch()<<" "<<pChild->IsParent(pTreeNode)<<" "<<pChild->IsParent(pTreeNode33)<<std::endl;}bEmpty = cTreeBinSeq.IsEmpty();std::cout<<bEmpty<<std::endl;dwDegree = cTreeBinSeq.GetDegree();std::cout<<dwDegree<<std::endl;dwHeight = cTreeBinSeq.GetHeight();std::cout<<dwHeight<<std::endl;dwNodesNum = cTreeBinSeq.GetNodesNum();std::cout<<dwNodesNum<<std::endl;AL_ListSeq<DWORD> cListSeq;DWORD dwData;BOOL bSibling = cTreeBinSeq.GetSiblingAtNode(pTreeNode, cListSeq);if (TRUE == bSibling) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();bSibling = cTreeBinSeq.GetSiblingAtNode(pTreeNode20, cListSeq);if (TRUE == bSibling) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();BOOL bAncestor = cTreeBinSeq.GetAncestorAtNode(pRootNode, cListSeq);if (TRUE == bAncestor) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}bAncestor = cTreeBinSeq.GetAncestorAtNode(pTreeNode33, cListSeq);if (TRUE == bAncestor) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();BOOL bDescendant = cTreeBinSeq.GetDescendantAtNode(pRootNode, cListSeq);if (TRUE == bDescendant) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();bDescendant = cTreeBinSeq.GetDescendantAtNode(pTreeNode33, cListSeq);if (TRUE == bDescendant) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();BOOL bOrder = cTreeBinSeq.PreOrderTraversal(cListSeq);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();bOrder = cTreeBinSeq.InOrderTraversal(cListSeq);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();bOrder = cTreeBinSeq.PostOrderTraversal(cListSeq);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();bOrder = cTreeBinSeq.LevelOrderTraversal(cListSeq);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData)) {std::cout<<dwData<<", ";}}std::cout<<std::endl;}cListSeq.Clear();BOOL bConvertToHuffman = cTreeBinSeq.ConvertToHuffman();std::cout<<bConvertToHuffman<<std::endl;AL_ListSeq<DWORD> cListSeqWeight;bOrder = cTreeBinSeq.LevelOrderTraversal(cListSeq, cListSeqWeight);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData) && TRUE == cListSeqWeight.Get(dwCnt, dwWeight)) {std::cout<<"["<<dwData<<", "<<dwWeight<<"]"<<", ";}}std::cout<<std::endl;}cListSeq.Clear();cListSeqWeight.Clear();dwDegree = cTreeBinSeq.GetDegree();std::cout<<dwDegree<<std::endl;dwHeight = cTreeBinSeq.GetHeight();std::cout<<dwHeight<<std::endl;dwNodesNum = cTreeBinSeq.GetNodesNum();std::cout<<dwNodesNum<<std::endl;cTreeBinSeq.RemoveNode(pTreeNode20);bConvertToHuffman = cTreeBinSeq.ConvertToHuffman();std::cout<<bConvertToHuffman<<std::endl;bOrder = cTreeBinSeq.LevelOrderTraversal(cListSeq, cListSeqWeight);if (TRUE == bOrder) {for (DWORD dwCnt=0; dwCnt<cListSeq.Length(); dwCnt++) {if (TRUE == cListSeq.Get(dwCnt, dwData) && TRUE == cListSeqWeight.Get(dwCnt, dwWeight)) {std::cout<<"["<<dwData<<", "<<dwWeight<<"]"<<", ";}}std::cout<<std::endl;}bEmpty = cTreeBinSeq.IsEmpty();std::cout<<bEmpty<<std::endl;dwDegree = cTreeBinSeq.GetDegree();std::cout<<dwDegree<<std::endl;dwHeight = cTreeBinSeq.GetHeight();std::cout<<dwHeight<<std::endl;dwNodesNum = cTreeBinSeq.GetNodesNum();std::cout<<dwNodesNum<<std::endl;#endif