实对称矩阵为正定矩阵的一个充分必要条件
本文是为了在学习凸优化的时候遇到的一个问题展开讨论的。目的是能够明白凸优化的理论基础，或者尽可能的明白它的理论基础。
1，对称矩阵的特征值是实数。
证明如下：（我是用latex编辑的，这里不能显示公式，所以我只能用图片了。
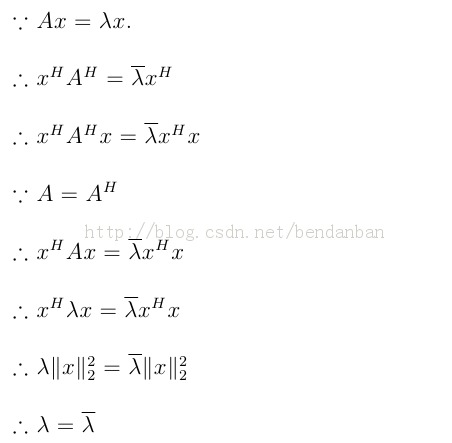
上面的证明可以说明对称矩阵的特征值一定是实数！
2、n阶方阵一定有n个特征跟（重跟按重数计算）
证明：
设A是一个n阶的方阵，它的特征多项式
是一个关于符号lambda的一个n次多项式，根据代数基本定理，它可以唯一的分解成一次因式的乘积。所以
一定有n个复数跟。
3、n阶实对称矩阵一定有n个实特征跟（重跟按重数计算）
由1和2便可以得到这个结论。
4、对称矩阵，从属于不同特征值的特征向量正交。
证明：
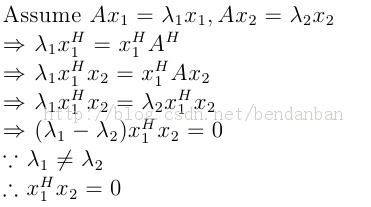
5、设A为n阶对称矩阵，则必有正交矩阵P，使得P^{-1}AP = P'AP = B，其中B是以A的特征值为对角线元素的对角矩阵。
这个不证明。
6、n阶对称阵的k重特征值的特征空间的维数是k。
7、对称矩阵所有特征向量以及零向量可以组成的线性空间还是原空间！
8、总上结论，我们可以得到结论：
实对称矩阵是非负定矩阵的充分必要条件是它的所有特征值都非负！！！
实对称矩阵是正定矩阵的充分必要条件是它的所有特征值都大于0！！！
上面两个结论只需要用正定矩阵的定义和实对称矩阵的性质证明。
