利用尾递归减少栈空间的消耗
首先,需要给出一个定义,什么是尾递归。在《算法精解》中给出的定义如下:
如果一个函数中所有递归形式的调用都出现在函数的末尾,我们称这个递归函数是尾递归的。当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时,这个递归调用就是尾递归的。尾递归函数的特点是在回归过程中不用做任何操作,这个特性很重要,因为大多数编译器会利用这个特点自动生成优化的代码。
看完上面这段描述,是不是觉得和没说差不多,看不明白。好吧,那就看看下面这张图吧。
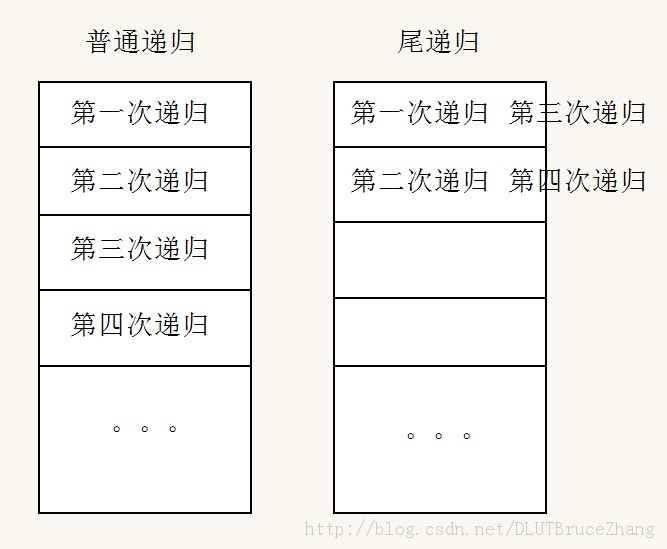
这张图的左面是正常的递归,我们可以看到,越往深一层(即函数自身被调用一次),栈就要被多消耗掉一部分空间。而右边这张图,只有两次递归需要用到不同的栈空间,其余都是上次的空间被直接覆盖掉。
下面,我们利用普通的递归和尾递归计算一个表达式:
1 + 1/2 + 1/3 + 1/4 + .... + 1/n
代码如下:
#include <stdio.h>double pi(double n);double pitail(double n, double a);int main(int argc, char *argv[]){printf("%lf\n", pi(5));printf("%lf\n", pitail(5, 0));return 0;}double pi(double n){if (n == 0) {return -1;} else if (n == 1) {return n;} else if (n > 1) {return pi(n-1) + 1/n;}}double pitail(double n, double a){if (n == 0) {return -1;} else if (n == 1) {return a + 1;} else if (n > 1) {return pitail(n-1, a + 1/n);}}