Swing数独游戏(2)：终盘生成之随机法

Swing数独游戏(二)：终盘生成之随机法
在上一篇博文介绍了用矩阵转换法来产生数独终盘。关于矩阵转换法产生终盘矩阵请参考如下的文章。

Swing数独游戏(一)：终盘生成之矩阵转换法 ==> http://mouselearnjava.iteye.com/blog/1941483

本篇博文将对数独游戏随机产生数独终盘展开说明。

用什么样的随机方法？

读过一些文章，关于随机产生数据终盘比较流行的是将拉斯维加斯算法与回溯法相结合。比如下面的文章都有提及：

http://zhangroup.aporc.org/images/files/Paper_3485.pdf
http://wenku.baidu.com/view/f9e3f17101f69e31433294e1.html



看了如下PPT: Java算法http://wenku.baidu.com/view/0a67634de518964bcf847c80.html





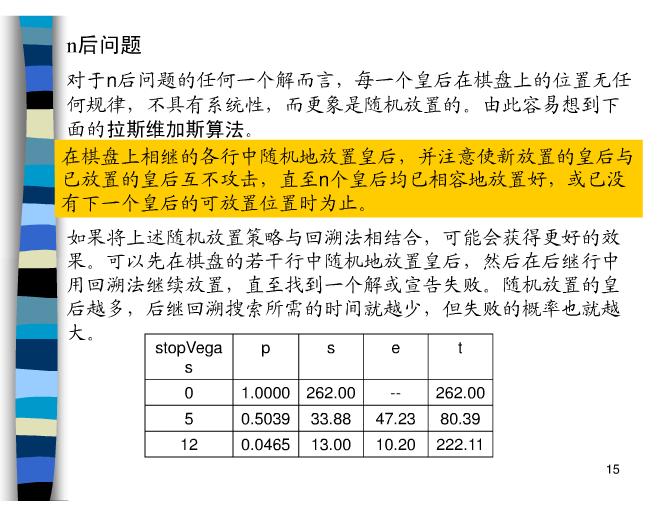
从上面的两个PPT截图中可以看出，拉斯维加斯算法思想去解决N皇后时所花费的时间不少。
数独中的判断不比N皇后少，如果想要在1秒内或者更短的时间产生1000个数独终盘，个人觉得并不是很容易（当然了，这个希望以后去证明一下是正确的）。

所以，我想选择另外的途径去完成。

我的随机方法思想

在给出我的随机方法思想之前，我们先来看看数独终盘的数量。

终盘数量

终盘数量数独中的数字排列千变万化，那么究竟有多少种终盘的数字组合呢？
6,670,903,752,021,072,936,960（约有6.67×10的21次方）种组合，2005年由Bertram Felgenhauer和Frazer Jarvis计算出该数字，并将计算方法发布在他们网站上，如果将等价终盘（如旋转、翻转、行行对换，数字对换等变形）不计算，则有5,472,730,538个组合。数独终盘的组合数量都如此惊人，那么数独题目数量就更加不计其数了，因为每个数独终盘又可以制作出无数道合格的数独题目。
-- 参考自http://baike.baidu.com/link?url=ePXUCvpBaRKBkEA3pVfOkg3m-NBozO6a4GDS0N3E5_gK1nnJCDzd5O-YL1w7c5S3


按照这个数量，如果我们将一个[1,2,3,4,5,6,7,8,9]的数组随机化，然后将其作为一行数据添加到一个二维数组中去，该行能满足数独终盘规则的概率是很大的。

基于这个假设(假设的有效性会在文章后面验证)，我的随机算法思想如下：

1. 写一个方法用于获取一个由1到9九个数随机排列的一维数组。2. 循环行(下标从0到8)，将这个随机产生的一维数组作为当前行的内容，如果是第一行（行标为0），那么直接作为该行的内容。如果是其它行，则验证数据是否都符合条件。   如果符合条件，则再产生一个由1到9九个数随机排列的一维数组作为下一行的内容并验证数据是否可用。   如果不符合条件，则将该行数据设置为0，调整row和col，产生一个由1到9九个数随机排列的一维数组，重新对该行验证。3. 程序中为了防止产生一维随机数组的方法调用很多次而没有产生结果，设置一个最多调用该方法次数的阈值，当达到这个阈值还没有产生结果，重新从 row =0  col =0  开始。

实现的程序如下：

从上面的结果图中可以看出：[b]300个实例中，调用次数最小的为11，接近理想最小调用次数9.

最大值为217次，平均约50次。而且大部分实例调用的次数在100以内。

从这些数据分析中，上述假设基本上是合适的，阈值最后选择了接近实验最大值217的220.[/b]

效果和结论

选择产生不同的数目的数独终盘，看看执行的时间。





结论：

1. 在打印二维数组到控制台显示的情况下，产生10万个随机数独终盘的时间差不多1分钟左右。
2. 在打印二维数组到控制台显示的情况下，产生1000个随机数独终盘的时间差不到1秒，这个正是我们之前所期望的。
3. 产生大数目的随机终盘，将二维数组打印到控制台显示的时间占据总时间的60%左右。
如果不在控制台输出二维数组，花费的时间将少很多。 看上面的折线就可以知道。

总的来说，效果还是比较不错的，比较适合一下需要产生很多的数独终盘的情况，比如：初始化1000个或者更多个数独终盘并写入文件，然后作为数独游戏的每关内容。

在下一篇博文中将介绍使用“挖洞”的思想去生成数独难题。

使用在Console打印出随机产生二维矩阵的的测试代码，及其产生50000个和100000个二维矩阵的结果截图如下：[/b]









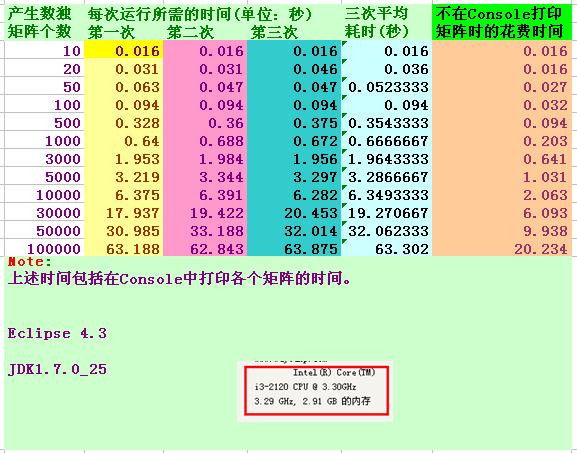
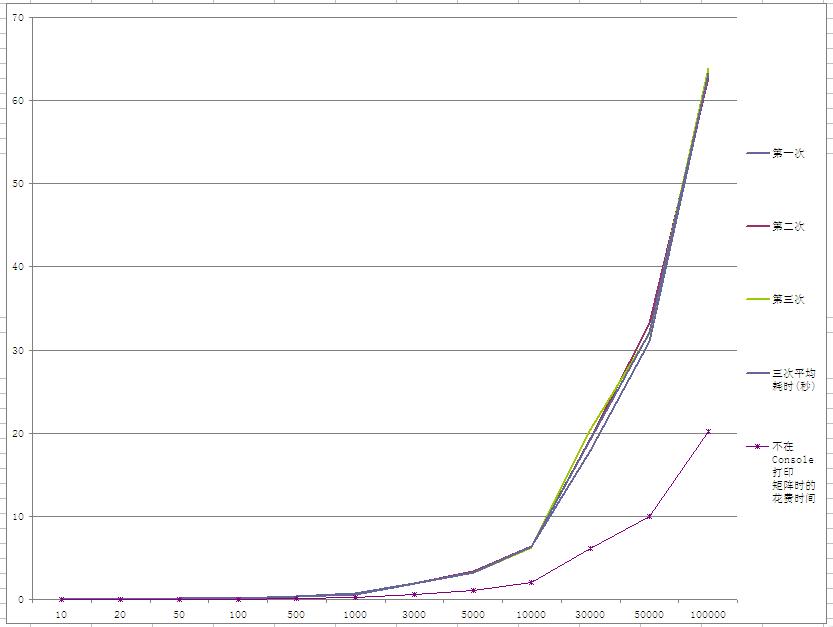
在下一篇博文中将介绍使用“挖洞”的思想去生成数独难题。

转载请注明出处：http://mouselearnjava.iteye.com/blog/1941693