GDI+坐标系中秋矩形的中心点~

2013-08-01

【求助】GDI+坐标系中秋矩形的中心点~~~~~~~~~~已知一条边上的两个点的坐标（不是对角点），和矩形的长宽，求在G

【求助】GDI+坐标系中秋矩形的中心点~~~~~~~~~~
已知一条边上的两个点的坐标（不是对角点），和矩形的长宽，求在GDI+坐标系中矩形的中心点坐标，
上图，图已经画好了，不过矩形的倾斜角度未知（也不确定）：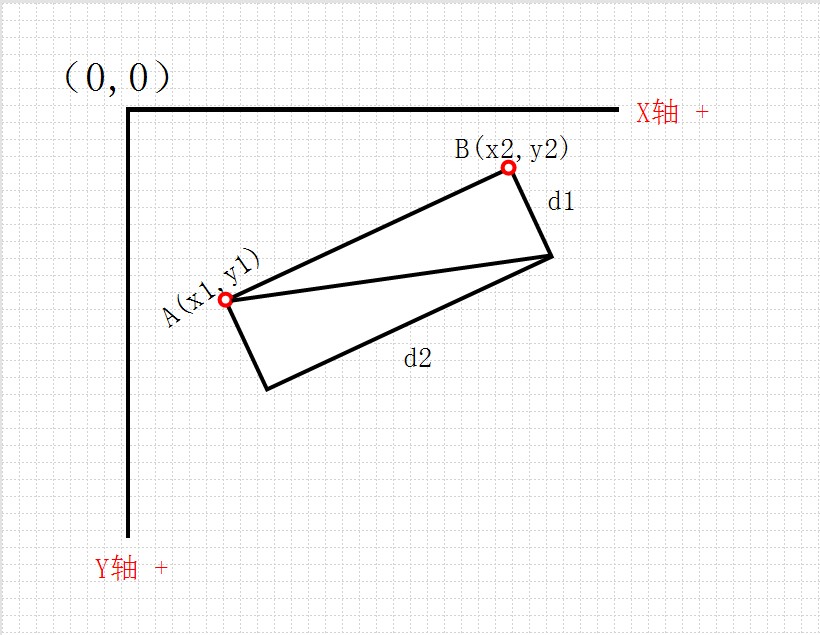

希望更给出推导公式，数学全忘了......

GDI+坐标系中秋矩形的中心点~

[解决办法]
还是写出Y的公式吧.
C点值:
Cx=(x1+x2)/2;
Cy=(y1+y2)/2;

SinA=(y2-y1)/d2;
CosA=(x2-x1)/d2;

中心x=Cx + (d1/2) * SinA;
中心y=Cy + (d1/2) * CosA;

代进去

中心x=Cx + (d1/2) * (y2-y1)/d2;
中心y=Cy + (d1/2) * (x2-x1)/d2;

[解决办法]

引用:

Quote: 引用:

还是写出Y的公式吧.
C点值:
Cx=(x1+x2)/2;
Cy=(y1+y2)/2;

SinA=(y2-y1)/d2;
CosA=(x2-x1)/d2;

中心x=Cx + (d1/2) * SinA;
中心y=Cy + (d1/2) * CosA;

代进去

中心x=Cx + (d1/2) * (y2-y1)/d2;
中心y=Cy + (d1/2) * (x2-x1)/d2;

点A 点B代表一条向量，那么这个向量的角度该怎么求呢？A-->B的向量......这个我忘了怎么求了，是从B到A 求夹角还是直接 A-->B呢....

这个角解不需要求出来,如果要求出角值就慢了.
只需要一个比例值就可以啦.
中心x=(x1+x2)/2 + (d1/2) * (y2-y1)/d2;

中心y=(y1+y2)/2 + (d1/2) * (x2-x1)/d2;

其中d2也是可以求出来的.就两点间的长度,是可能通过x1,y1 x2,y2求得的. 但d1的长度必须给定.
[解决办法]
不需要太多的什么向量知识啦,就初二的搞定啦..
好好看看下图: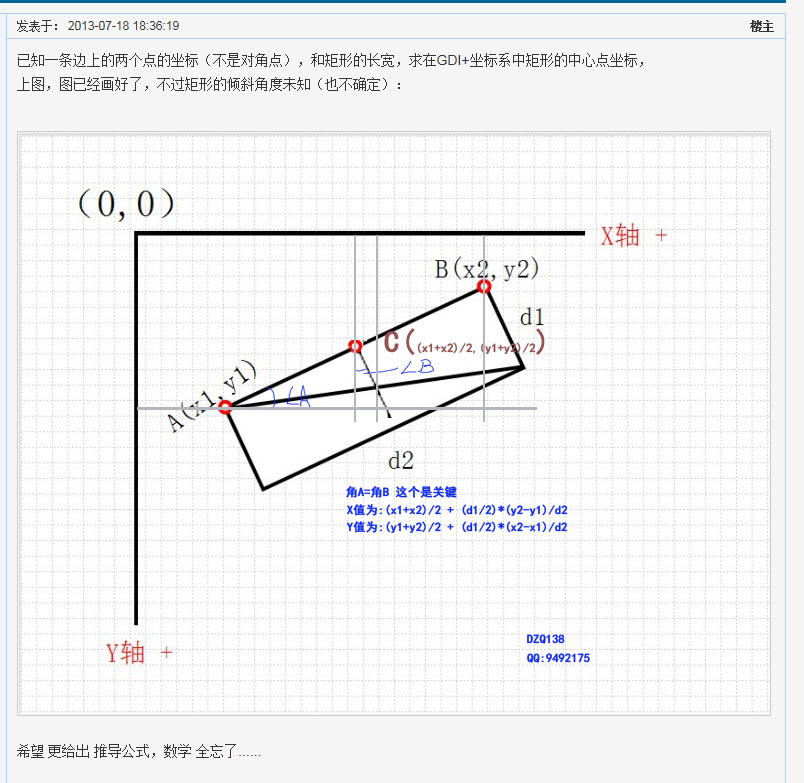
GDI+坐标系中秋矩形的中心点~
[解决办法]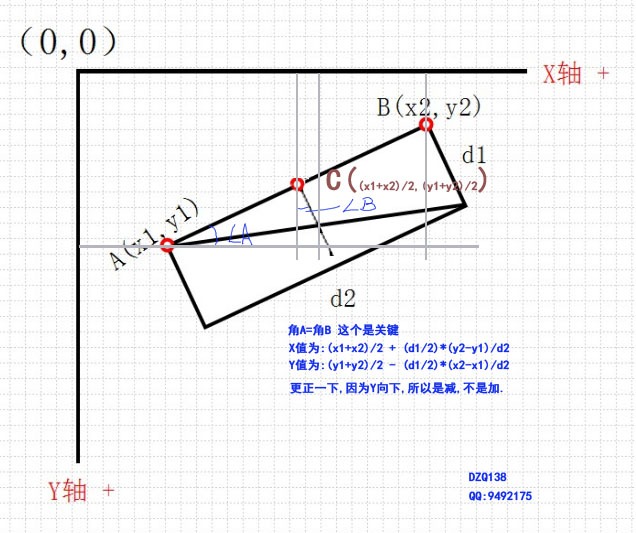

[解决办法]
向量是您如果要点跟线和线与线的关系.
都是一些快速判断几何关系。
如:

[解决办法]

[解决办法]
           . p2(x2,y2)

[解决办法]

[解决办法]

[解决办法]
  . p1(x1,y1)

[解决办法]

------------------------------
(0,0)

p1p2的矢量为 (x2-x1,y2-y1)

[解决办法]

[解决办法]
           . Q(x2,y2)

[解决办法]

[解决办法]

[解决办法]
     . P(x1,y1)

[解决办法]
o
------------------------------
(0,0)

点积(内积) 线段PO与QO的夹角有以下关系:
P.Q=x1*x2 + y1*y2 =
[解决办法]
P
[解决办法]
Q
[解决办法]
cos(P,Q)
P与Q不共线,则有
PQ>0 则P与Q的夹角>90度
PQ<0 则P与Q的夹角<90度
PQ=0 则P与Q的夹角=90度

再对叉积.
P1P2与OP的叉积
(x2-x1)*y3 - (y2-y1)*x3
等于0,则共线.
反证与您的要求没有什么关联...
都是一些快速判断几何关系。

热点排行

软件架构设计

GDI+坐标系中秋矩形的中心点~