两道微软笔试题求解~~~~ 大家来看看吧
两道微软笔试题求解~~~~ 大家来看看吧
1. Find the number of different shotest paths from point A to point B in a city with
perfectly horizontal streets and vertical avenues as shown in the following figure. No path can cross the fenced off area shown in gray in the figure.
A. 11
B. 15
C. 17
D. 19
E. 20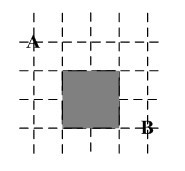
2 An algorithm starts with a single equilateral triangle and on each subsequent iteration add new triangles all around the outside. The result for the first three values of n are shown following figure. How many small triangles will be there after the 100 iterations?
A 19800
B 14501
C 14851
D 14702
E 15000
从 A 出发到蓝点的不同走法数为 f(4,2),到达蓝点后只有一种走法,即一直向右到 B。
从 A 出发到红点的不同走法数为 f(2,4),到达后再到 B 点的不同走法数为 f(3,2),因此连接的总数为 f(2,4)*f(3,2)。
至此,唯一没有涵盖的走法为经黑点至 B,此种走法有且只有一种。
因此总数目为 f(4,2) + f(2,4)*f(3,2) + 1 == 17.
2. C
设 dn 为第 n 次新增加的小三角形数目,则
n == 1, d1 = 1.
n == 2, d2 = 3.
n == 3, d3 = 6.
n == 4, d4 = 9.
n == 5, d5 = 12.
猜测模式为 1,3,6,9,12,15,... 即 n==2 后为等差数列,通向公式为
d(n) = 3(n-1), n>=2.
则总三角形数目为
1 + sigma(n==2..100,3(n-1)) == 14851.