0015算法笔记——多边形游戏问题
1、问题描述:
给定N个顶点的多边形,每个顶点标有一个整数,每条边上标有+(加)或是×(乘)号,并且N条边按照顺时针
依次编号为1~N。下图给出了一个N=4个顶点的多边形。
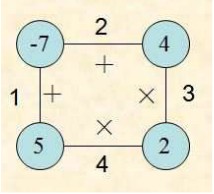
游戏规则 :(1) 首先,移走一条边。 (2) 然后进行下面的操作: 选中一条边E,该边有两个相邻的顶点,不妨称为V1和V2。对V1和V2顶点所标的整数按照E上所标运算符号(+或是×)进行运算,得到一个整数;用该整数标注一个新顶点,该顶点代替V1和V2 。 持续进行此操作,直到最后没有边存在,即只剩下一个顶点。该顶点的整数称为此次游戏的得分(Score)。
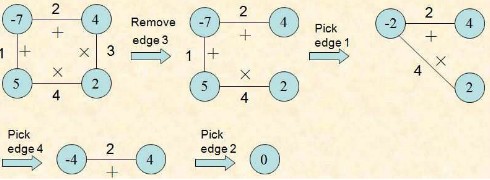
2、问题分析:
解决该问题可用动态规划中的最优子结构性质来解。
设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中,op[i]表示第i条边所对应的运算符,v[i]表示第i个顶点上的数值,i=1~n。
在所给的多边形中,从顶点i(1<=i<=n)开始,长度为j(链中有j个顶点)的顺时针链p(i,j)可表示为v[i],op[i+1],…,v[i+j-1],如果这条链的最后一次合并运算在op[i+s]处发生(1<=s<=j-1),则可在op[i+s]处将链分割为两个子链p(i,s)和p(i+s,j-s)。
设m[i,j,0]是链p(i,j)合并的最小值,而m[i,j,1]是最大值。若最优合并在op[i+s]处将p(i,j)分为两个长度小于j的子链的最大值和最小值均已计算出。即:
a=m[i,s,0] b=m[i,s,1] c=m[i,s,0] d=m[i,s,1]
(1) 当op[i+s]=’+’时
m[i,j,0]=a+c ;m[i,j,1]=b+d
(2) 当op[i+s]=’*’时
m[i,j,0]=min{ac,ad,bc,bd} ; m[i,j,1]=max{ac,ad,bc,bd}
由于最优断开位置s有1<=s<=j-1的j-1中情况。 初始边界值为 m[i,1,0]=v[i] 1<=i<=n m[i,1,1]=v[i] 1<=i<=n
因为多变形式封闭的,在上面的计算中,当i+s>n时,顶点i+s实际编号为(i+s)modn。按上述递推式计算出的m[i,n,1]记为游戏首次删除第i条边后得到的最大得分。
算法具体代码如下:
//3d6 多边形游戏#include "stdafx.h"#include <iostream> using namespace std; #define NMAX 100int N,m[NMAX+1][NMAX+1][2],v[NMAX+1]; char op[NMAX+1];void MinMax(int n,int i,int s,int j,int &minf,int &maxf);int PloyMax(int n,int& p);int main() { int p;cout<<"请输入多边形顶点数:"<<endl;cin>>N;for(int i=1; i<=N; i++){cout<<"请输入多边形顶点"<<i<<"数值:"<<endl;cin>>v[i]; m[i][1][0]=v[i]; m[i][1][1]=v[i]; cout<<"请输入多边形边"<<i<<"运算符:"<<endl;cin>>op[i]; } cout<<"多边形游戏首次删除第"<<p<<"条边,结果为:"<<PloyMax(N,p)<<endl; return 0;}void MinMax(int n,int i,int s,int j,int &minf,int &maxf){ int e[5];int a=m[i][s][0],b=m[i][s][1];int r=(i+s-1)%n+1;//多边形的实际顶点编号int c=m[r][j-s][0],d=m[r][j-s][1];if(op[r-1]=='+'){ minf=a+c;maxf=b+d;} else{ e[1]=a*c;e[2]=a*d;e[3]=b*c; e[4]=d*b; minf=e[1]; maxf=e[1]; for(int r=2;r<N;r++) { if(minf>e[r])minf=e[r];if(maxf<e[r])maxf=e[r];}}}int PloyMax(int n,int& p){ int minf,maxf;for(int j=2;j<=n;j++) //迭代链的长度{for(int i=1;i<=n;i++)//迭代首次删掉第i条边{for(int s=1 ;s<j;s++) //迭代断开位置{ MinMax(n,i,s,j,minf,maxf);if(m[i][j][0]>minf) m[i][j][0]=minf; if(m[i][j][1]<maxf) m[i][j][1]=maxf;} }}int temp=m[1][n][1]; p=1;for(int i=2 ;i<=n; i++) { if(temp<m[i][n][1]) {temp=m[i][n][1];p=i;}} return temp;} 程序运行结果如下:
