第 三 部分: 深入推荐引擎相关算法 - 聚类
第 3 部分: 深入推荐引擎相关算法 - 聚类??df-count 目录:保存着文本的频率信息tf-vectors 目录:保存着以
第 3 部分: 深入推荐引擎相关算法 - 聚类
?
?
- df-count 目录:保存着文本的频率信息
- tf-vectors 目录:保存着以 TF 作为权值的文本向量
- tfidf-vectors 目录:保存着以 TFIDF 作为权值的文本向量
- tokenized-documents 目录:保存着分词过后的文本信息
- wordcount 目录:保存着全局的词汇出现的次数
- dictionary.file-0 目录:保存着这些文本的词汇表
- frequcency-file-0 目录 : 保存着词汇表对应的频率信息。
介绍完向量化问题,下面我们深入分析各个聚类算法,首先介绍的是最经典的 K 均值算法。
?
介绍完 K 均值聚类算法,我们可以看出它最大的优点是:原理简单,实现起来也相对简单,同时执行效率和对于大数据量的可伸缩性还是较强的。然而缺点也是很明确的,首先它需要用户在执行聚类之前就有明确的聚类个数的设置,这一点是用户在处理大部分问题时都不太可能事先知道的,一般需要通过多次试验找出一个最优的 K 值;其次就是,由于算法在最开始采用随机选择初始聚类中心的方法,所以算法对噪音和孤立点的容忍能力较差。所谓噪音就是待聚类对象中错误的数据,而孤立点是指与其他数据距离较远,相似性较低的数据。对于 K 均值算法,一旦孤立点和噪音在最开始被选作簇中心,对后面整个聚类过程将带来很大的问题,那么我们有什么方法可以先快速找出应该选择多少个簇,同时找到簇的中心,这样可以大大优化 K 均值聚类算法的效率,下面我们就介绍另一个聚类方法:Canopy 聚类算法。
?
?
计算 v 到其他簇的相关性只需将 d1替换为对应的距离。
从上面的算式,我们看出,当 m 近似 2 时,相关性近似 1;当 m 近似 1 时,相关性近似于到该簇的距离,所以 m 的取值在(1,2)区间内,当 m 越大,模糊程度越大,m 就是我们刚刚提到的模糊参数。
讲了这么多理论的原理,下面我们看看如何使用 Mahout 实现模糊 K 均值聚类,同前面的方法一样,Mahout 一样提供了基于内存和基于 Hadoop Map/Reduce 的两种实现 FuzzyKMeansClusterer 和 FuzzyMeansDriver,分别是清单 5 给出了一个例子。
清单 5. 模糊 K 均值聚类算法示例
?
?
Mahout 实现的狄利克雷聚类算法是按照如下过程工作的:首先,我们有一组待聚类的对象和一个分布模型。在 Mahout 中使用 ModelDistribution 生成各种模型。初始状态,我们有一个空的模型,然后尝试将对象加入模型中,然后一步一步计算各个对象属于各个模型的概率。下面清单给出了基于内存实现的狄利克雷聚类算法。
清单 6. 狄利克雷聚类算法示例
?
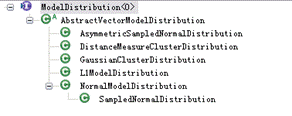
Mahout 中提供多种概率分布模型的实现,他们都继承 ModelDistribution,如图 4 所示,用户可以根据自己的数据集的特征选择合适的模型,详细的介绍请参考 Mahout 的官方文档。
图 4 Mahout 中的概率分布模型层次结构
 ?
?
参考资料
学习
- 聚类分析:Wikipedia 上关于聚类分析的介绍
- 数据挖掘:概念与技术(韩家伟):关于数据挖掘的经典著作,详细介绍了数据挖掘领域的各种问题和应用,其中对聚类分析的经典算法也有详尽的讲解。
- 数据挖掘:实用机器学习技术:同样是数据挖掘的经典著作,对领域内的算法,算法的发展进行了详细的介绍。
- “Apache Mahout简介” (Grant Ingersoll,developerWorks,2009 年 10 月):Mahout 的创始者 Grant Ingersoll 介绍了机器学习的基本概念,并演示了如何使用 Mahout 来实现文档集群、提出建议和组织内容。
- Apache Mahout:Apache Mahout 项目的主页,搜索关于 Mahout 的所有内容。
- Apache Mahout算法总结:Apache Mahout 的 Wiki 上关于实现算法的详细介绍。
- Mahout In Action:Sean Owen 详细介绍了 Mahout 项目,其中有很大篇幅介绍了 Mahout 提供的聚类算法,并给出一些简单的例子。
- TF-IDF:Wikipedia 上关于 TF-IDF 的详细介绍,包括它的计算方法,优缺点,应用场景等。
- 路透数据集:路透提供了大量的新闻数据集,可以作为聚类分析的数据源,本文中对文本聚类分析的部分采用了路透“Reuters-21578”数据集
- Efficient Clustering of High Dimensional Data Sets with Application to Reference Matching,发表于 2000 的 Canopy 算法的论文。
- 狄利克雷分布:Wikipedia 上关于狄利克雷分布的介绍,它是本文介绍的狄利克雷聚类算法的基础
- 基于Apache Mahout构建社会化推荐引擎:笔者 09 年发布的一篇关于基于 Mahout 实现推荐引擎的 developerWorks 文章,其中详细介绍了 Mahout 的安装步骤,并给出一个简单的电影推荐引擎的例子。
- 机器学习:机器学习的 Wikipedia 页面,可帮助您了解关于机器学习的更多信息。
- developerWorks Java技术专区:数百篇关于 Java 编程各个方面的文章。?
- developerWorks Web development 专区:通过专门关于 Web 技术的文章和教程,扩展您在网站开发方面的技能。
- developerWorks Ajax 资源中心:这是有关 Ajax 编程模型信息的一站式中心,包括很多文档、教程、论坛、blog、wiki 和新闻。任何 Ajax 的新信息都能在这里找到。
- developerWorks Web 2.0 资源中心,这是有关 Web 2.0 相关信息的一站式中心,包括大量 Web 2.0 技术文章、教程、下载和相关技术资源。您还可以通过?Web 2.0 新手入门?栏目,迅速了解 Web 2.0 的相关概念。
- 查看?HTML5 专题,了解更多和 HTML5 相关的知识和动向。
 ?
?