第 2 部分: 深入推荐引擎相关算法 - 协同过滤
可以看出,当 n=2 时,欧几里德距离就是平面上两个点的距离。
当用欧几里德距离表示相似度,一般采用以下公式进行转换:距离越小,相似度越大
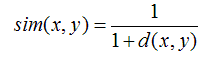
皮尔逊相关系数一般用于计算两个定距变量间联系的紧密程度,它的取值在 [-1,+1] 之间。
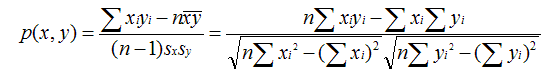
sx, sy是 x 和 y 的样品标准偏差。
Cosine 相似度被广泛应用于计算文档数据的相似度:
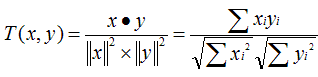
Tanimoto 系数也称为 Jaccard 系数,是 Cosine 相似度的扩展,也多用于计算文档数据的相似度:
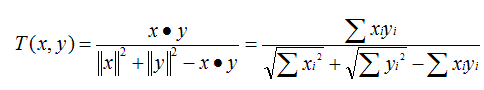
相似邻居的计算
介绍完相似度的计算方法,下面我们看看如何根据相似度找到用户 - 物品的邻居,常用的挑选邻居的原则可以分为两类:图 1 给出了二维平面空间上点集的示意图。
不论邻居的“远近”,只取最近的 K 个,作为其邻居。如图 1 中的 A,假设要计算点 1 的 5- 邻居,那么根据点之间的距离,我们取最近的 5 个点,分别是点 2,点 3,点 4,点 7 和点 5。但很明显我们可以看出,这种方法对于孤立点的计算效果不好,因为要取固定个数的邻居,当它附近没有足够多比较相似的点,就被迫取一些不太相似的点作为邻居,这样就影响了邻居相似的程度,比如图 1 中,点 1 和点 5 其实并不是很相似。
与计算固定数量的邻居的原则不同,基于相似度门槛的邻居计算是对邻居的远近进行最大值的限制,落在以当前点为中心,距离为 K 的区域中的所有点都作为当前点的邻居,这种方法计算得到的邻居个数不确定,但相似度不会出现较大的误差。如图 1 中的 B,从点 1 出发,计算相似度在 K 内的邻居,得到点 2,点 3,点 4 和点 7,这种方法计算出的邻居的相似度程度比前一种优,尤其是对孤立点的处理。
图 1.相似邻居计算示意图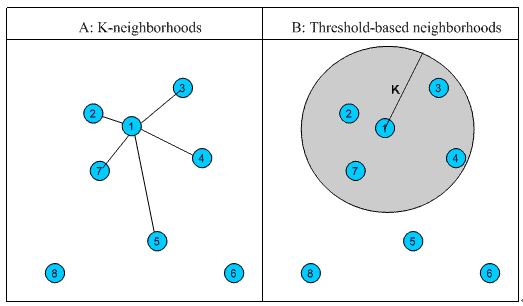 ?
?
?
基于物品的 CF(Item CF)
基于物品的 CF 的原理和基于用户的 CF 类似,只是在计算邻居时采用物品本身,而不是从用户的角度,即基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他。从计算的角度看,就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度,得到物品的相似物品后,根据用户历史的偏好预测当前用户还没有表示偏好的物品,计算得到一个排序的物品列表作为推荐。图 3 给出了一个例子,对于物品 A,根据所有用户的历史偏好,喜欢物品 A 的用户都喜欢物品 C,得出物品 A 和物品 C 比较相似,而用户 C 喜欢物品 A,那么可以推断出用户 C 可能也喜欢物品 C。
图 3.基于物品的 CF 的基本原理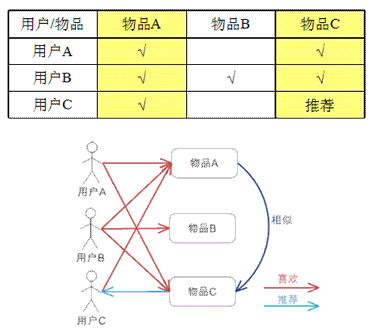 ?
?
User CF vs. Item CF
前面介绍了 User CF 和 Item CF 的基本原理,下面我们分几个不同的角度深入看看它们各自的优缺点和适用场景:
Item CF 和 User CF 是基于协同过滤推荐的两个最基本的算法,User CF 是很早以前就提出来了,Item CF 是从 Amazon 的论文和专利发表之后(2001 年左右)开始流行,大家都觉得 Item CF 从性能和复杂度上比 User CF 更优,其中的一个主要原因就是对于一个在线网站,用户的数量往往大大超过物品的数量,同时物品的数据相对稳定,因此计算物品的相似度不但计算量较小,同时也不必频繁更新。但我们往往忽略了这种情况只适应于提供商品的电子商务网站,对于新闻,博客或者微内容的推荐系统,情况往往是相反的,物品的数量是海量的,同时也是更新频繁的,所以单从复杂度的角度,这两个算法在不同的系统中各有优势,推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。
在非社交网络的网站中,内容内在的联系是很重要的推荐原则,它比基于相似用户的推荐原则更加有效。比如在购书网站上,当你看一本书的时候,推荐引擎会给你推荐相关的书籍,这个推荐的重要性远远超过了网站首页对该用户的综合推荐。可以看到,在这种情况下,Item CF 的推荐成为了引导用户浏览的重要手段。同时 Item CF 便于为推荐做出解释,在一个非社交网络的网站中,给某个用户推荐一本书,同时给出的解释是某某和你有相似兴趣的人也看了这本书,这很难让用户信服,因为用户可能根本不认识那个人;但如果解释说是因为这本书和你以前看的某本书相似,用户可能就觉得合理而采纳了此推荐。
相反的,在现今很流行的社交网络站点中,User CF 是一个更不错的选择,User CF 加上社会网络信息,可以增加用户对推荐解释的信服程度。
研究推荐引擎的学者们在相同的数据集合上分别用 User CF 和 Item CF 计算推荐结果,发现推荐列表中,只有 50% 是一样的,还有 50% 完全不同。但是这两个算法确有相似的精度,所以可以说,这两个算法是很互补的。
关于推荐的多样性,有两种度量方法:
第一种度量方法是从单个用户的角度度量,就是说给定一个用户,查看系统给出的推荐列表是否多样,也就是要比较推荐列表中的物品之间两两的相似度,不难想到,对这种度量方法,Item CF 的多样性显然不如 User CF 的好,因为 Item CF 的推荐就是和以前看的东西最相似的。
第二种度量方法是考虑系统的多样性,也被称为覆盖率 (Coverage),它是指一个推荐系统是否能够提供给所有用户丰富的选择。在这种指标下,Item CF 的多样性要远远好于 User CF, 因为 User CF 总是倾向于推荐热门的,从另一个侧面看,也就是说,Item CF 的推荐有很好的新颖性,很擅长推荐长尾里的物品。所以,尽管大多数情况,Item CF 的精度略小于 User CF, 但如果考虑多样性,Item CF 却比 User CF 好很多。
如果你对推荐的多样性还心存疑惑,那么下面我们再举个实例看看 User CF 和 Item CF 的多样性到底有什么差别。首先,假设每个用户兴趣爱好都是广泛的,喜欢好几个领域的东西,不过每个用户肯定也有一个主要的领域,对这个领域会比其他领域更加关心。给定一个用户,假设他喜欢 3 个领域 A,B,C,A 是他喜欢的主要领域,这个时候我们来看 User CF 和 Item CF 倾向于做出什么推荐:如果用 User CF, 它会将 A,B,C 三个领域中比较热门的东西推荐给用户;而如果用 ItemCF,它会基本上只推荐 A 领域的东西给用户。所以我们看到因为 User CF 只推荐热门的,所以它在推荐长尾里项目方面的能力不足;而 Item CF 只推荐 A 领域给用户,这样他有限的推荐列表中就可能包含了一定数量的不热门的长尾物品,同时 Item CF 的推荐对这个用户而言,显然多样性不足。但是对整个系统而言,因为不同的用户的主要兴趣点不同,所以系统的覆盖率会比较好。
从上面的分析,可以很清晰的看到,这两种推荐都有其合理性,但都不是最好的选择,因此他们的精度也会有损失。其实对这类系统的最好选择是,如果系统给这个用户推荐 30 个物品,既不是每个领域挑选 10 个最热门的给他,也不是推荐 30 个 A 领域的给他,而是比如推荐 15 个 A 领域的给他,剩下的 15 个从 B,C 中选择。所以结合 User CF 和 Item CF 是最优的选择,结合的基本原则就是当采用 Item CF 导致系统对个人推荐的多样性不足时,我们通过加入 User CF 增加个人推荐的多样性,从而提高精度,而当因为采用 User CF 而使系统的整体多样性不足时,我们可以通过加入 Item CF 增加整体的多样性,同样同样可以提高推荐的精度。
前面我们大部分都是从推荐引擎的角度考虑哪个算法更优,但其实我们更多的应该考虑作为推荐引擎的最终使用者 -- 应用用户对推荐算法的适应度。
对于 User CF,推荐的原则是假设用户会喜欢那些和他有相同喜好的用户喜欢的东西,但如果一个用户没有相同喜好的朋友,那 User CF 的算法的效果就会很差,所以一个用户对的 CF 算法的适应度是和他有多少共同喜好用户成正比的。
Item CF 算法也有一个基本假设,就是用户会喜欢和他以前喜欢的东西相似的东西,那么我们可以计算一个用户喜欢的物品的自相似度。一个用户喜欢物品的自相似度大,就说明他喜欢的东西都是比较相似的,也就是说他比较符合 Item CF 方法的基本假设,那么他对 Item CF 的适应度自然比较好;反之,如果自相似度小,就说明这个用户的喜好习惯并不满足 Item CF 方法的基本假设,那么对于这种用户,用 Item CF 方法做出好的推荐的可能性非常低。
通过以上的介绍,相信大家已经对协同过滤推荐的各种方法,原则,特点和适用场景有深入的了解,下面我们就进入实战阶段,重点介绍如何基于 Apache Mahout 实现协同过滤推荐算法。
??
Slope One 的核心优势是在大规模的数据上,它依然能保证良好的计算速度和推荐效果。Mahout 提供了 Slope One 推荐方法的基本实现,实现代码很简单,参考清单 5.
清单 5. 基于 Mahout 实现 Slope One
学习