【矩阵乘法再实践】HDU 2604——queuing
题目:点击打开链接
首先,这是一个递推问题。mm结尾的只能由fm结尾的或者mm结尾的推来。以mf结尾的只能由mm结尾的推来,以fm结尾的只能由mf或者ff推来,以ff结尾的只能由mf推来。
F(n)=F(n-1)+F(n-3)+F(n-4)。可是正常用大数的话会TLE。后来查阅DISCUSS得知应该使用矩阵乘法。
其中1——4是已知的。
其中这个A矩阵是要构建的,一般是通过0-1阵,达到下图的目的,构阵方式不唯一。
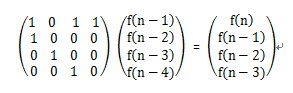
构完阵后,将目标值-4,然后进行二分幂优化,再手动把前四加上,还是稍微有点晕的,毕竟数学略拙计。。
另外附两个较为清楚的大神链接:
矩阵乘法的方法 DP的方法
#include <iostream>#include <cmath>#include <cstring>using namespace std;class Mat{public: __int64 mat[10][10];};int n=4; //维度,即矩阵A的行数int MOD;//好多问题要求给出取余之后的数字Mat E;int f[5]={0,2,4,6,9};void initE(){for(int i=0;i<10;i++)E.mat[i][i]=1;}Mat operator*(Mat a,Mat b){ int i,j,k; Mat c; for (i=0;i<n;i++) { for (j=0;j<n;j++) { c.mat[i][j] = 0; for (k=0;k<n;k++) c.mat[i][j]+=(a.mat[i][k]*b.mat[k][j])%MOD; c.mat[i][j]%=MOD; } } return c;}Mat operator+(Mat a,Mat b){ Mat c; int i,j; for (i=0;i<n;i++) { for (j=0;j<n;j++) c.mat[i][j] = (a.mat[i][j]+b.mat[i][j])%MOD; } return c;}Mat operator^(Mat a,int x) { Mat p = E,q = a; while (x>=1) { if(x%2==1) p = p*q; x/=2; q = q*q; } return p; }Mat solve(Mat a,int p) { if(p==1) return a; else if(p&1) return (a^p)+solve(a,p-1); else return ((a^(p>>1))+E)*solve(a,p>>1); } int main() { int length,mod; while(cin>>length>>MOD) { initE();Mat a;memset(a.mat,0,sizeof(a.mat)); a.mat[0][0]=a.mat[0][2]=a.mat[0][3]=a.mat[1][0]=a.mat[2][1]=a.mat[3][2]=1; if(length<=4) { cout<<f[length]%MOD<<endl; continue; } Mat x; x=a^(length-4); int ans=0; ans=(x.mat[0][0]*9+x.mat[0][1]*6+x.mat[0][2]*4+x.mat[0][3]*2); cout<<ans%MOD<<endl; } return 0; }