字符串匹配:KMP & AC 自动机个人学习总结
字符串匹配问题
给定两个字符串,其中一个文本串T[1..n], 另一个是模式串P[1...m]。确定T中是否存在与P串完全相等的(连续的)子串,若有,输出T中和P完全匹配的子串的起始位置。 模板题 HDU 1711点这里。
给定若干个字符串,其中一个是文本串T[1...n],其他的都是模式串Pi[1....mi]。确定T中有多少个子串和其中一个Pi完全相等。输出所有匹配结果。 模板题 HDU 2222 点这里
对于第一个问题——单模式串匹配
朴素匹配算法: 用一个循环枚举T[1....n]中所有的起点1~n, 将T从起点开始和P[1...m]匹配。最坏情况是每一个T起点都匹配到P 的最后一个然后失败,如T = aaaa……..aaab, P = aaaaaaaab。故复杂度O(n*m)。很多时候这样的算法复杂度不能满足题目要求例如上面的例题。 不过这种起点逐个尝试的思路是其他字符串匹配算法的基础。PS:(可能说的不好,未能体现KMP的精髓,不过都是本人自学的心得。见谅~)
KMP算法: KMP算法可以拥有线性的算法复杂度上界,其过程并不复杂,只是需要用到上面朴素匹配算法没用到的一种重要性质。
先来定义一点东西:定义一个前缀函数π(T):返回一个长度—— T的真后缀(比T短的后缀)和T的真前缀相等中长度最大值。
就是最大的k使得T[1...k] = T[k-n+1.....n].
例如T = ababa, 则π(T)= 3
ababa
ababa
显然总是有π(T) < T.len ; T的长度len。
KMP算法思想
假设T[s+1....s+k] 与P [1..k] 已经匹配。如果k==m那么返回匹配完成。
如果k<m呢?< span="">
N:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
T: b a c b a b a b a a b c b a b…..
P: a b a b a c a
如上,P的前5个字符已经和T的匹配,而接下来的第六个匹配却失败了。
按照朴素匹配算法,此时会从T的5号位置从新开始对P匹配。
然而朴素的算法忽略了一些信息:P的前5个字符已经匹配成功的事实可以确定T中相应的位置的信息,而KMP算法正是利用这些信息立即得知某些新的起始位置是非法的(也就是说从这个起点出发不可能有成功的匹配),排除掉这些非法起始位置同时可以迅速得知P在新位置的匹配情况,有效提高算法效率。
以下部分建议拿出纸和笔自行画图模拟。再多的文字描述不如画图来的实际。
如果P已经完成 1 ~ k 的匹配,k+1匹配失败,如何正确确定新的起始位置呢?按照原来假设
有T [ s + 1 ... s + k ] = P[ 1 ... k ] π( P [ 1 ... k ] ) = t。显然 t < k 。这时候只需要将模式串P右移使得P串t长的前缀刚好和本来位置t长的P1后缀重合,然后继续让T[s+k+1]和P[t+1]开始匹配就行了。为什么可以这样呢?首先可以证明:P这样的右移(右移了k-t)是最少量的合法右移。这意味着右移量(1….k-t+1)都是不合法的。下面图片是粗略的证明过程。
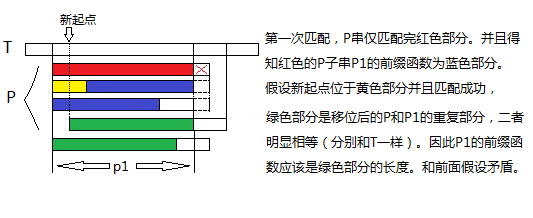
知道这一性质,可以认为每次失败匹配后,P可以跳过许多非法起点而直接从s+k-t+1开始。即模式串P向右移动k – t 位(也就是上图P应直接移动到黄色部分以后的蓝色部分开始匹配)。因为前缀函数的定义,移位后的P可以和移位前T停止的地方重新开始匹配。(因为移位后P的前缀就和本来的后缀重合了)。确定了移动位置之后,又再用相同的策略来考虑新的匹配。
如此KMP算法可以分成以下两步:
1.先求得给定模式串P[1....m]每一个前缀函数。
2.用T从1号开始和P匹配。
遇到匹配失败的时候就按照上面说到的操作移动P。继续按照相同的策略匹配。
具体在写算法的时候,可以用两个指针 i , j 分别指着P 和T 。按照上面的步骤,当T[i] == P[j]的时候i 和j 同时像右移。否则,就应该让P向右移使得P[1..k]的π(k)长的前后缀重合。相当于是i 指向 π(i)。这里还有一个问题:P[1...m]的每一个前缀函数怎么求得?其实求P的前缀函数过程与T和P匹配的过程是很相像的(可以参看我的模板,二者真的很像……),至于怎么实现就留着当做一点思考吧,理解了之后会对KMP有更好的认识。
我的模板(字符串从0开始,各种参数都和推导结果不一样):
#include <iostream>#include <cstdio>#include<limits.h>#include <cmath>#include <cstdlib>#include <cstring>#include <algorithm>using namespace std;const int N = 100000 + 5;char s[N], p[N];long long fail[N], cnt[N], res1[N], res2[N];void Rev(char str[]){ int i = 0, j = strlen(str) - 1; char t; while(i < j) { t = str[i]; str[i] = str[j]; str[j] = t; i++; j--; }}void Get_fail(){ int i = -1; fail[0] = -1; for(int j = 0; p[j];) { while(i != -1 && p[i] != p[j]) i = fail[i]; i++; j++; fail[j] = i; }}void KMP(){ int i = 0; for(int j = 0; s[j]; ) { while(i != -1 && s[j] != p[i]) i = fail[i]; i++; j++; cnt[i] ++; }}void Get_res(long long res[], int len){int i; for(i = len; i > 0; i--) { res[i] = cnt[i]; cnt[fail[i]] += cnt[i]; }}int main(){ int Cas; scanf("%d", &Cas); while(Cas--) { memset(cnt, 0, sizeof(cnt)); memset(res1, 0, sizeof(res1)); memset(res2, 0, sizeof(res2)); scanf("%s%s", s, p); int len = strlen(p); Get_fail(); KMP(); Get_res(res1, len); Rev(s); Rev(p);memset(cnt, 0, sizeof(cnt)); Get_fail(); KMP(); Get_res(res2, len); long long ans = 0; for(int i = 1; i < len; i++) { ans += res1[i] * res2[len - i]; } printf("%lld\n", ans); } return 0;}==========华丽的分割线================
对于第二个问题——多模式串匹配:
这个问题和上面第一个问题相比,只多了一种条件——模式串P的个数,他们形成一个集合SP。可以沿用KMP算法来解决,分别将T和每一个模式串匹配,统计匹配的次数 ,当匹配完成后i指针回归fail[i]。这是一个可行的方法,复杂度会是O(n*|SP| ) ,然而对于上面的第二个模板题,这种复杂度是不可以接受的。这时候我们就需要用到一种新的算法:AC自动机。
我初学AC自动机的时候是拜读了NotOnlySuccess 大神(orz。。。。) 的博客里面的一份论文。给出博客传送门自己去下载吧,我就不盗链了……:传送门。正如NotOnlySuccess大神所说:网上有好多阐述AC自动机算法的博客不过都没有说的很好的,而那份论文能严谨而面面俱到,看了会让人有茅塞顿开的感觉。所以还是强力建议直接去啃那份极品论文吧。看完之后直接切他博客的题目好了,都是好题。另外我自己将那篇论文搞了篇译文:《Biosequence Algorithms, Spring 2005 Lecture 4: Set Matching and Aho-Corasick Algorithm》 欢迎阅读。