poj pku 1673 EXOCENTER OF A TRIANGLE 三角形 垂心
题目描述:http://poj.org/problem?id=1673[size=large][/size]
该题重点是求证点O 为△ABC的垂心
延长BO 交AC 与R, 先证OR⊥AC(其它AO⊥BC, CO⊥AB 同理)
见下图: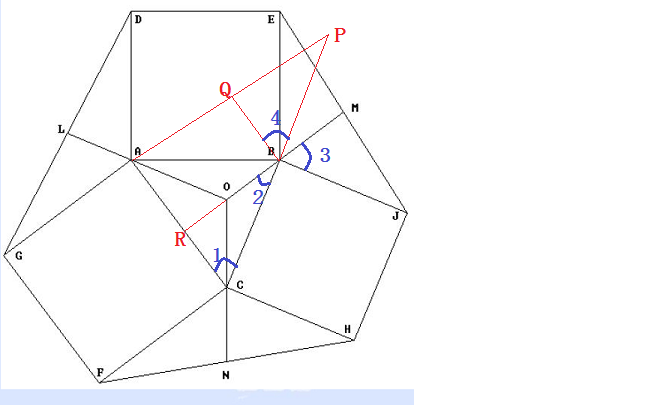
1) 绕点B 旋转△EBJ, 使BE 与 BA 重合,得△ABP, 则△EBJ≌△ABP
2) 因为∠ABC 与 ∠EBJ 互余,所以旋转后点P、B、C 共线,且点B 为PC 中点
3) 记AP 中点为Q,则BQ 为中位线,所以∠1 = ∠4
4) 又∠4 为∠3旋转得到,显然∠4 = ∠3,则∠1 = ∠3
5) 显然∠2 与∠3 互余(∠CBJ 为90°), 又∠1 = ∠3,所以∠2 与∠1 互余
所以OR⊥AC
证毕
#include <cstdio>#include <cmath>#define eps 1e-8struct point {double x, y;};struct line {point a, b;};//返回二阶行列式的值double xmult(double a1, double a2, double b1, double b2) {return a1 * b2 - a2 * b1;}//返回线段的交点, 先确保两直线不共线(平行、重合)//先把直线表示成ax + by + c = 0 的形式point intersection(line u, line v) {double a1, b1, c1, a2, b2, c2;a1 = u.b.y - u.a.y;b1 = u.a.x - u.b.x;c1 = u.b.x * u.a.y - u.a.x * u.b.y;a2 = v.b.y - v.a.y;b2 = v.a.x - v.b.x;c2 = v.b.x * v.a.y - v.a.x * v.b.y;//注意精度控制, 好像g++ 和 vc 的表现不同。c++(vc)能AC, g++ 就不行了//不知道为什么, 请高人指点point ret;ret.x = xmult(b1, b2, c1, c2) / xmult(a1, a2, b1, b2) + eps;ret.y = -1.0 * xmult(a1, a2, c1, c2) / xmult(a1, a2, b1, b2) + eps;return ret;}//返回两点间的距离double distance(point p1, point p2) {return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));}//返回a, b, c 三点组成的三角形的垂心//前提: a, b, c 三点不共线point perpencenter(point a, point b, point c) {line u, v;u.a = c;u.b.x = u.a.x - a.y + b.y;u.b.y = u.a.y + a.x - b.x;v.a = b;v.b.x = v.a.x - a.y + c.y;v.b.y = v.a.y + a.x - c.x;return intersection(u, v);}int main() {int ncase;point a, b, c, ans;scanf("%d", &ncase);while (ncase--) {scanf("%lf %lf %lf %lf %lf %lf", &a.x, &a.y, &b.x, &b.y, &c.x, &c.y);ans = perpencenter(a, b, c);printf("%.4lf %.4lf\n", ans.x, ans.y);}return 0;}