谈谈模型的选择
在我们运用机器学习解决实际问题时,我们可能用得最多的套路就是找特征,选模型,扔进去训练。比如当我们面对{0,1}分类问题时,我们可能很自然的就想到了逻辑回归来解决,但是这个看似自然的做法背后又是怎么得来的呢?为什么我们要选择逻辑回归呢?又比如,很多文章中都用到的关于房屋价格的回归问题时,我们可能也会很快就想到最小二乘法,同样,这又是怎么得来的呢?这里,我将给出一些非常漂亮的理由。同时,同样的方法也可以用在其它类似的机器学习算法中的模型选择问题上。
为了后面描述方便,我们首先简单回顾一下指数分布簇的函数形式,
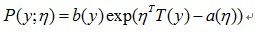
千万别被这个公式吓跑了,其实在这里,我们并不会去深究指数分布簇各个参数的意义,暂且只需要知道有这回事就ok了。因为我们介绍它只是为了引出广义线性模型的定义,因为我们前面所提到的逻辑回归,最小二乘等,都属于广义线性模型中的一个特例。所以,通过广线性模型来最终引出为什么我们在解决这类问题时选择这两个模型,并且得出类似问题的解决方法,应该是比较合理的。广义线性模型(GLM)定义为需要满足如下三个条件:
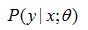 满足指数分布簇的分布;
满足指数分布簇的分布;
给定x, 我们的目标是想得到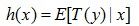
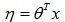
好了,现在我们可以正式介绍当我们面对一个{0,1}分类问题时,我们是怎么知道最终采用逻辑回归模型来解决。我们知道,当y属于{0,1}最为自然的分布就是伯努利分布,因此,有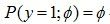 。下面有几步推导,相信只要有一点数学功底的都能够看得懂。
。下面有几步推导,相信只要有一点数学功底的都能够看得懂。
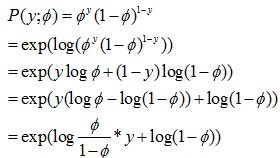
有人会问了,我们推导出这个式子有什么作用呢?别急,作用可大了。细心的同学会发现,其实最后的等式就是一个指数分布簇的形式。伯努利分布就是一个指数分布簇的特例。这里,
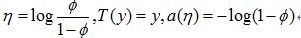
仔细观察,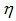 是以
是以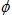 为自变量的函数,稍作变形可以得到:
为自变量的函数,稍作变形可以得到: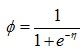 。
。
回到我们一开始对广义线性模型的定义,我们已经证明了伯努利分布满足了广义线性模型的第一条性质。对第二条性质,给定了x和theta,我们想要得到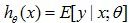 ,显然,对伯努利分布,这个期望值就是等于以theta为参数,给定x条件下y=1的概率(因为y=0的期望项为0)。因此,
,显然,对伯努利分布,这个期望值就是等于以theta为参数,给定x条件下y=1的概率(因为y=0的期望项为0)。因此,
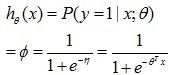
这就是我们的逻辑回归模型!我们通过一系列的还不算复杂的推导,从观察到的最简单直接的0,1事件,得到了逻辑回归模型来建模。当然后序就可以通过极大似然等方法,得到我们的训练迭代规则了。
我们再回到房屋价格预测这个问题上,我们一般都会看到对此类问题利用最小二乘法做如下建模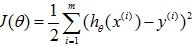 ,并且最小化它,通过梯度下降法或牛顿法都可以求得最终的迭代解。我们这里就会看到这样看似理所应当的理论背后的一些秘密。
,并且最小化它,通过梯度下降法或牛顿法都可以求得最终的迭代解。我们这里就会看到这样看似理所应当的理论背后的一些秘密。
一般,对房屋价格预测中,有各种各样的因素都会决定房屋的价格,比如卖家的情绪、买家的情绪、季节等等,我们对这些不可预知的因素都会假定是独立的,我们假定最终房屋价格满足高斯分布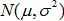 ,即:
,即: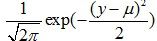 ,因此,我们有:
,因此,我们有:
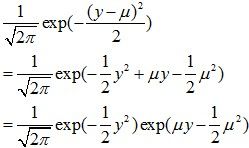
同上面一样,高斯分布也是一个指数分布簇的特例,其中:
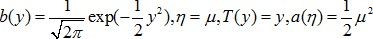
因此,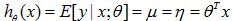 ,这就是我们对房屋价格所建立的模型,当然,别忘了加上随机满足高斯分布的不可预知的因素
,这就是我们对房屋价格所建立的模型,当然,别忘了加上随机满足高斯分布的不可预知的因素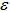 ,即:
,即: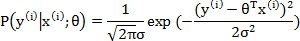 。利用极大似然:
。利用极大似然: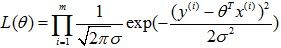 得到:
得到:
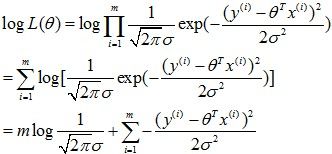
因此,最大化似然函数就相当于最小化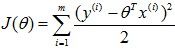 ,这就是我们的最小二乘了。
,这就是我们的最小二乘了。
好了,到了这里,我想有必要总结一下,当我们遇到一个问题时,假如需要预测的问题又恰好只能取两个值时,我们需要做出的唯一决策就是使用伯努利分布,同理,我们也可以假定y属于不同的分布,比如高斯分布、伽玛分布,泊松分布等,遵从相似的算法,就可以得到不同的机器学习模型了。最后我们只需要处理训练集合了,利用最大似然,梯度下降,牛顿等,得到我们的参数迭代公式。