深入理解二分查找(一、二分查找及其变体)
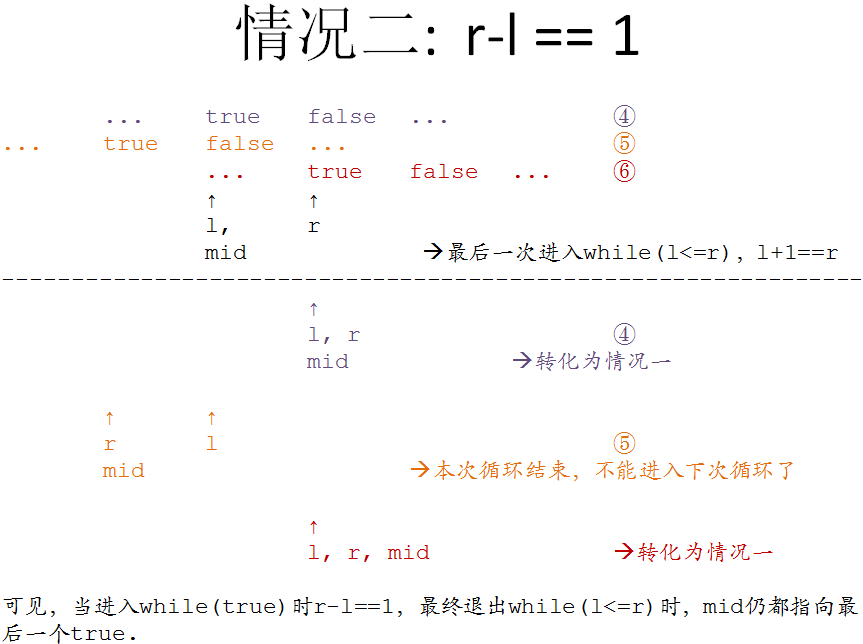
???????? 《编程之美》2.19解法二需要在一个数组arr[]中找到最后一个≤value的值,可以顺序查找,也可以使用二分查找。但标准的二分查找用来查找=value的值,因此这里需要改造一下:
?
?
代码:??? 综上,调用bin_search(arr, 0, len),将返回最后一个true的位置;若不存在true则返回0.
??? 我的解题思路是这样的矩阵行列都是从小到大排好序的,要查找的话自然用二分效率比较高,而且这样的矩阵有个性质,最左上角的元素必定是最小值,最右下角的是最大值,在一个n*n的矩阵中,对角线的元素也是排好序的,找到对角线上的一个元素,使得这个元素小于待查找的key,并且下一元素大于待查找的key,那么只要在这个元素的左下角矩阵和右上角矩阵递归继续对角线查找就可以了,例如上图例子里查找7,只要找到对角线的元素4,然后递归查找红圈的矩阵就可以了 ,左上角矩阵最大值4<7,右下角矩阵最小值10>7,无需查找了。
??? 但是此题并没有告诉我们原始矩阵是n*n的,这是比较麻烦的地方,不过思路是一样的,无非不能用对角线查找这样简单的办法了,假设m*n的矩阵,对角线查找的办法改进为i = (m1+m2)/2,j = (n1+n2)/2 进行查找就可以了,(m1,n1)为矩阵最左上角元素下标,(m2,n2)为最右下角元素下标
?
总结一下基本思路:
(1)对于n*n的有序二维数组:? 函数bin_search()在对角线上运用“二分”过程,找到i使得a[i][i]<k<a[i+1][i+1],然后对于“a[i][i]的左下角矩阵”和“a[i][i]的右上角矩阵”分别递归调用bin_search()查找即可。
(2)对于m*n的有序二维数组:? 基本同上,只是bin_search()不是对对角线“二分”,而是对矩阵m*n进行“二分缩放”(Sam: 这个词是我发明的:)示意图如下)
贴一下(2)的代码:
int bin_search(int value, int *a, int n, int m1, int n1, int m2, int n2){ int begin_m1 = m1, begin_n1 = n1, end_m2 = m2, end_n2 = n2; int left_result = 0, right_result = 0; int i = (m1+m2)/2, j = (n1+n2)/2; if (a == NULL) return 0; if (value < *(a+m1*n+n1) || value > *(a+m2*n+n2)) return 0; else if (value == *(a+m1*n+n1) || value == *(a+m2*n+n2)) return 1; while ((i!=m1 || j!=n1) && (i!=m2 || j!=n2)){ if ( value == *(a+i*n+j) ) return 1; else if ( value < *(a+i*n+j) ){ m2 = i; n2 = j; i = (i+m1)/2; j = (j+n1)/2; } else{ m1 = i; n1 = j; i = (i+m2)/2; j = (j+n2)/2; } } //search left & right if ( i<end_m2 ) left_result = bin_search(value, a, n, i+1, begin_n1, end_m2, j); if ( j<end_n2 ) right_result = bin_search(value, a, n, begin_m1, j+1, i, end_n2); if (left_result | right_result ) return 1; else return 0;}顺便提一句,我先前还看到一个笨娃娃说:可以变量所有的a[][]的行,对每一列进行二分查找,这样的复杂度是O(nlog(n)),呜呼!当然不错啦,但一看就学艺不精。
?
?