POJ 3525 Most Distant Point from the Sea(半平面交+二分)
转载请注明出处,谢谢http://blog.csdn.net/acm_cxlove/article/details/7854526 by---cxlove
题目:一个多边形,求出到边界最近的距离的最大值。
http://poj.org/problem?id=3525
题目转换成在多边形内可以画一个最大半径为多少的圆。
二分答案半径,然后判断是否存在这样一个区域能放入这个圆心。
每次在半平面交的时候把面向内侧平移半径长度,然后判断新的多边形是否存在核。
看一下每次向内推进r的坐标变换
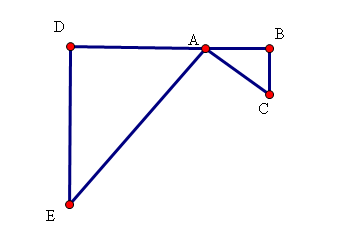
已经这个图中将AE边推进长度为R,也就是A点最C点,那么我们要求的是C点的坐标或者坐标的变化值
也就是AB,和BC的长度。
已经A,E点坐标(XA,YA)(XB,YB),已经AC长度R。
可以发现三角形ADE与三角形CBA相似。而已知AE坐标也就已知AD,DE长度,便可以得到AB,BC长度。
问题解决 ,剩下的就是基础的半平面交
#include<iostream>#include<fstream>#include<iomanip>#include<cstdio>#include<cstring>#include<algorithm>#include<cstdlib>#include<cmath>#include<set>#include<map>#include<queue>#include<stack>#include<string>#include<vector>#include<sstream>#include<cassert>#define LL long long#define eps 1e-5#define inf 1<<30using namespace std;struct Point{ double x,y;}p[1505],tp[1505],q[1505];//叉积double xmul(Point p0,Point p1,Point p2){ return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);}//通过两点,确定直线方程double Get_equation(Point p1,Point p2,double &a,double &b,double &c){ a=p2.y-p1.y; b=p1.x-p2.x; c=p2.x*p1.y-p1.x*p2.y;}//求交点Point Intersection(Point p1,Point p2,double a,double b,double c){ double u=fabs(a*p1.x+b*p1.y+c); double v=fabs(a*p2.x+b*p2.y+c); Point t; t.x=(p1.x*v+p2.x*u)/(u+v);t.y=(p1.y*v+p2.y*u)/(u+v); return t;}//求面积,正为顺时针,和叉积写法有关double Get_area(Point p[],int n){ double area=0; for(int i=2;i<n;i++) area+=xmul(p[1],p[i],p[i+1]); return -area/2.0;}//改变顺序double Change_dir(Point p[],int n){ for(int i=1;i<=n/2;i++) swap(p[i],p[n+1-i]);}//加入一条边,切割void Cut(double a,double b,double c,Point p[],int &cnt){ int tmp=0; for(int i=1;i<=cnt;i++){ //当前点就在右侧 if(a*p[i].x+b*p[i].y+c>-eps) tp[++tmp]=p[i]; else{ //前一个点在右侧,产生交点 if(a*p[i-1].x+b*p[i-1].y+c>eps) tp[++tmp]=Intersection(p[i-1],p[i],a,b,c); //同理 if(a*p[i+1].x+b*p[i+1].y+c>eps) tp[++tmp]=Intersection(p[i],p[i+1],a,b,c); } } for(int i=1;i<=tmp;i++) p[i]=tp[i]; p[0]=p[tmp];p[tmp+1]=p[1]; cnt=tmp;}int slove(Point q[],int n,double r){ //默认顺时针,通过面积判断一下 if(Get_area(q,n)<eps) Change_dir(q,n); q[0]=q[n];q[n+1]=q[1]; //原来的点要备份一遍,查了好久 for(int i=0;i<=n+1;i++) p[i]=q[i]; int cnt=n; for(int i=1;i<=n;i++){ double a,b,c; Point p1,p2,p3; p1.y=q[i].x-q[i+1].x;p1.x=q[i+1].y-q[i].y; double k=r/sqrt(p1.x*p1.x+p1.y*p1.y); p1.x=k*p1.x;p1.y=p1.y*k; p2.x=p1.x+q[i].x;p2.y=p1.y+q[i].y; p3.x=p1.x+q[i+1].x;p3.y=p1.y+q[i+1].y; Get_equation(p2,p3,a,b,c); Cut(a,b,c,p,cnt); } return cnt;}int main(){ int t,n,cas=0; while( scanf("%d",&n)!=EOF&&n){ for(int i=1;i<=n;i++) scanf("%lf%lf",&q[i].x,&q[i].y); double low=0,high=1<<30,mid; while(fabs(high-low)>eps){ mid=(low+high)/2.0; if(slove(q,n,mid)) low=mid; else high=mid; } printf("%.6f\n",mid); } return 0;}