平面最近点对问题详解
??? 在二维平面上的n个点中,如何快速的找出最近的一对点,就是最近点对问题。
??? 一种简单的想法是暴力枚举每两个点,记录最小距离,显然,时间复杂度为O(n^2)。
??? 在这里介绍一种时间复杂度为O(nlognlogn)的算法。其实,这里用到了分治的思想。将所给平面上n个点的集合S分成两个子集S1和S2,每个子集中约有n/2个点。然后在每个子集中递归地求最接近的点对。在这里,一个关键的问题是如何实现分治法中的合并步骤,即由S1和S2的最接近点对,如何求得原集合S中的最接近点对。如果这两个点分别在S1和S2中,问题就变得复杂了。
??? 为了使问题变得简单,首先考虑一维的情形。此时,S中的n个点退化为x轴上的n个实数x1,x2,...,xn。最接近点对即为这n个实数中相差最小的两个实数。显然可以先将点排好序,然后线性扫描就可以了。但我们为了便于推广到二维的情形,尝试用分治法解决这个问题。
??? 假设我们用m点将S分为S1和S2两个集合,这样一来,对于所有的p(S1中的点)和q(S2中的点),有p<q。
??? 递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2},并设
d = min{ |p1-p2| , |q1-q2| }
??? 由此易知,S中最接近点对或者是{p1,p2},或者是{q1,q2},或者是某个{q3,p3},如下图所示。
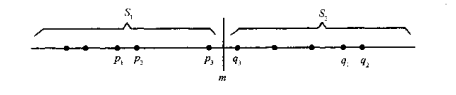
?
??? 如果最接近点对是{q3,p3},即|p3-q3|<d,则p3和q3两者与m的距离都不超过d,且在区间(m-d,d]和(d,m+d]各有且仅有一个点。这样,就可以在线性时间内实现合并。
??? 此时,一维情形下的最近点对时间复杂度为O(nlogn)。
??? 在二维情形下,类似的,利用分治法,但是难点在于如何实现线性的合并?
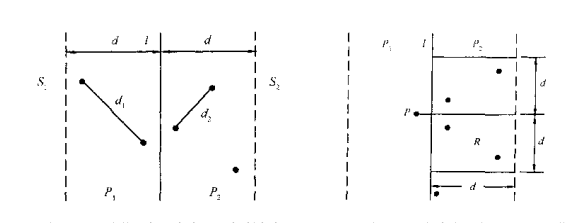
?
??? 由上图可见,形成的宽为2d的带状区间,最多可能有n个点,合并时间最坏情况下为n^2,。但是,P1和P2中的点具有以下稀疏的性质,对于P1中的任意一点,P2中的点必定落在一个d X 2d的矩形中,且最多只需检查六个点(鸽巢原理)。
??? 这样,先将带状区间的点按y坐标排序,然后线性扫描,这样合并的时间复杂度为O(nlogn),几乎为线性了。
?
??? 光说不练也不行,经过自己的思考和参考网上的程序,完成了最近点对的程序,并在各OJ上成功AC了。
??? POJ3714 ZOJ2107 HDU1007
/**最近点对问题,时间复杂度为O(n*logn*logn)*/#include <iostream>#include <cstdio>#include <cstring>#include <cmath>#include <algorithm>using namespace std;const double INF = 1e20;const int N = 100005;struct Point{ double x; double y;}point[N];int n;int tmpt[N];bool cmpxy(const Point& a, const Point& b){ if(a.x != b.x) return a.x < b.x; return a.y < b.y;}bool cmpy(const int& a, const int& b){ return point[a].y < point[b].y;}double min(double a, double b){ return a < b ? a : b;}double dis(int i, int j){ return sqrt((point[i].x-point[j].x)*(point[i].x-point[j].x) + (point[i].y-point[j].y)*(point[i].y-point[j].y));}double Closest_Pair(int left, int right){ double d = INF; if(left==right) return d; if(left + 1 == right) return dis(left, right); int mid = (left+right)>>1; double d1 = Closest_Pair(left,mid); double d2 = Closest_Pair(mid+1,right); d = min(d1,d2); int i,j,k=0; //分离出宽度为d的区间 for(i = left; i <= right; i++) { if(fabs(point[mid].x-point[i].x) <= d) tmpt[k++] = i; } sort(tmpt,tmpt+k,cmpy); //线性扫描 for(i = 0; i < k; i++) { for(j = i+1; j < k && point[tmpt[j]].y-point[tmpt[i]].y<d; j++) { double d3 = dis(tmpt[i],tmpt[j]); if(d > d3) d = d3; } } return d;}int main(){ while(true) { scanf("%d",&n); if(n==0) break; for(int i = 0; i < n; i++) scanf("%lf %lf",&point[i].x,&point[i].y); sort(point,point+n,cmpxy); printf("%.2lf\n",Closest_Pair(0,n-1)/2); } return 0;}?
?