微软一边笔试题 求数组中两个元素差的最大值（后面的元素减去前面的元素）O(N)时间复杂度O(1)空间复杂度

微软一面笔试题 求数组中两个元素差的最大值（后面的元素减去前面的元素）O(N)时间复杂度O(1)空间复杂度

自从暑假面试被鄙视之后，回来就经常想这个问题，到今天应该快两个月了。在这个下午，我又拿出草稿纸，总算找到了思路，把它给搞定了。就像一个心愿一样，完结了。问题是这样的，如同题目：原题就不赘述了，化简之后的问题就是在数组中找到两个元素，计算后面的元素减去前面的元素的差。求出所有差的最大值。（你可以认为你在炒股票，买入价格和卖出价格就是你的盈利）当时想到的方法是，如果一遍遍历这个数组，找到MAX,MIN元素，如果恰好，MAX在MIN的后面，这个问题就解决了，关键是如果这种情况不出现怎么办，我给出了递归的方法，回来自己想想发现不行，递归不靠谱，对一些测试用例来说很难有很高的效率。潜意识告诉我，求数组中连续元素的最大和的方法对这个问题有很大的启发，那个问题在本博客中已经解决过了，而且我反复做了两遍，太好了。那个问题的解决思路是将全部元素的问题，看成是从两个元素大小的数组开始的问题。当这个包含两个元素的问题解决了，那么加一个新的元素会造成什么影响？要改变哪些值？每次都添加一个元素，每次都将这些可能的改变考虑进来，这样就能做到遍历整个数组的时候，问题就结局了。达到了最快的速度O（N）有了上面的思路，这个问题居然更简单，其实现如下：

int max_difference(const vector<int>& arr){if (arr.size()>=2){int MIN=min(arr[0],arr[1]);int MAX_DIFFERENCE=arr[1]-arr[0];for (vector<int>::size_type i=2;i<arr.size();i++){if (arr[i]-MIN>MAX_DIFFERENCE){MAX_DIFFERENCE=arr[i]-MIN;}if (arr[i]<MIN){MIN=arr[i];}}return MAX_DIFFERENCE;}else{cout<<"size of arr is too small";return 0;}}void give_result(int a[],int n){vector<int> arr(a,a+n);print(arr.begin(),arr.end());print(max_difference(arr));}int main( void ) {int a0[]={7,9,10};give_result(a0,3);int a1[]={10,9,7};give_result(a1,3);int a[]={3,10,1,9};give_result(a,4);int a2[]={3,9,2,10,1,8};give_result(a2,6);return 0;}

其输出结果每两行作为一组，第一行为要考虑的数组的全部元素，第二行为其max_difference的结果。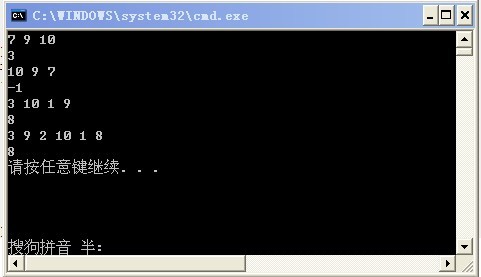

陆陆续续的做了不少笔试题，也感觉收获很大，但毕竟做的不够，这个是第一个用已经掌握的技巧解决的。感觉算法强大！！

细心的读者还会发现，本文中的代码使用了vector的逆序迭代器。以前做过类似算法要求的遍历使用正向迭代器总感觉别扭，忽然想起了逆序迭代器。发现真的适合这种情形。