贪心算法 - 单源最短路径 Dijkstra
单源最短路径:
一个带权有向图G=(V,E),其中n个顶点Vertex,以及连接各个顶点之间的边Edge,可能有些顶点之间没有边,每条边上的权值都是非负值。
给定其中的一个顶点,称之为源。
求出源到其他所有顶点之间的最短路径。
解法:
Dijkstra算法
以源为起始顶点集合S,向外扩张,
将从源到其他顶点且只经过S中顶点的路径,称为特殊路径。
每次都将S之外的顶点中的 特殊路径长度最短的顶点加入到S中,直到所有的顶点都已经在S中为止。
可以看出,该算法需要n-1步迭代,每次都会将一个顶点加入到S里。
以下图为例,1为源:
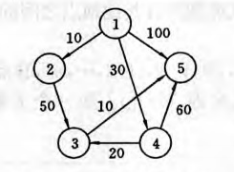
(1)S=[1]
初始情况
(2)S=[1,2]
[2,3,4,5]中2离S中最近,故将2放入S。
(3)S=[1,2,4]
[3,4,5]中4离S中最近,3离S得距离为60=10+50,4的距离为30,5的距离为100,故将4放入S中。
(4)s=[1,2,4,3]
[3,5]中3离S得距离为10+50=60,5的距离为30+60=90,故将3放入S中。
(5)S=[1,2,4,3,5]
结束。
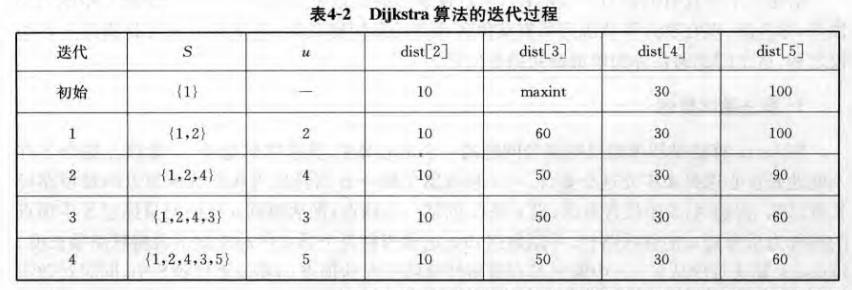
以邻接矩阵表示图。
[
[-1,10,-1,30,100],
[-1,-1,50,-1,-1],
[-1,-1,-1,-1,10],
[-1,-1,20,0,60],
[-1,-1,-1,-1,-1]
]
实现如下:
public class Dijkstra {public static final int NOT_REACHED = -1;/** * n vertexs * @param E n*n * @param source 0,1,2,3,...,n-1 */public static void dijkstra(int[][] E, int source) {int n = E.length;boolean[] S = new boolean[n]; // 标示各个顶点是否在S中int[] dist = new int[n]; // 保存source到各顶点,只经过S中顶点的路径的最短长度,如果没有这样的路径,为-1int[] prev = new int[n]; // 保存最短路径,的上一个顶点,以供回溯之用// 初始化distfor (int i = 0; i < n; i++) {dist[i] = E[source][i];S[i] = false;if (isReachable(E, source, i)) {prev[i] = source;} else {prev[i] = -1;}}S[source] = true;for (int i = 0; i < n; i++) {// 找出dist最小的int v = -1, j, min;// 先找第一个不在S中的for (j = 0; j < n && S[j]; j++) {}if (j == n)continue;v = j; // 第一个不在S中的min = dist[v];// 再找出dist最小的for (j = j + 1; j < n; j++) {if (!S[j] && dist[j] != -1 && dist[j] < min) {min = dist[j];v = j;}}S[v] = true; // 将dist最小的v放入S中for (j = 0; j < n; j++) {if (!S[j] && isReachable(E, v, j)&& (dist[j] == -1 || dist[v] + E[v][j] < dist[j])) {// 修订dist,看从v到各顶点的距离是否变短了dist[j] = dist[v] + E[v][j];prev[j] = v;}}for (j = 0; j < n; j++) {System.out.print(dist[j] + " ");}System.out.println();}}private static boolean isReachable(int[][] E, int v1, int v2) {return E[v1][v2] != NOT_REACHED;}public static void main(String[] args) {int[][] E = { { -1, 10, -1, 30, 100 }, { -1, -1, 50, -1, -1 },{ -1, -1, -1, -1, 10 }, { -1, -1, 20, 0, 60 },{ -1, -1, -1, -1, -1 } };dijkstra(E, 0);}}