Matrix简单使用
Matrix是一个3*3的矩阵: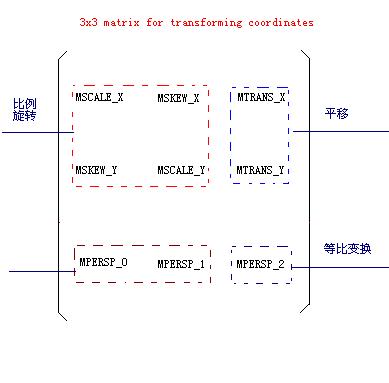
平移的矩阵计算:
现设点P0(x0, y0)进行平移后,移到P(x,y),其中x方向的平移量为△x,y方向的平移量为△y,那么,点P(x,y)的坐标为:
x = x0 + △x
y = y0 + △y
采用矩阵表达上述如下: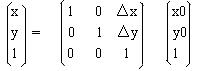
图像旋转的矩阵计算:
现设点P0(x0, y0)旋转θ角后的对有点为P(x, y)。通过使用向量,我们得到如下:
x0 = r cosα
y0 = r sinα
x = r cos(α-θ) = x0 cosθ+ y0 sinθ
y = r sia(α-θ) = -x0 sinθ+y0 cosθ
于是我们得到矩阵: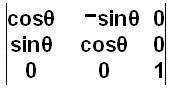
矩阵的放大缩小:
放大缩小是利用最下面的一行数值改变实现的。右下角的数值n>1表示缩放n,n<1表示扩展n倍
旋转和放大缩小是以当前左上角进行的。因此如果要以某点(x,y)旋转或者缩放,需要进行:
matrix.setScale(0.5f,0.5f);matrix.preTranslate(-x,-y);matrix.postTranslate(x,y);