单源最短路径之SPFA算法实现
这里来简单介绍下SPFA算法。
1、SPFA算法是求解单源最短路径的,时间复杂度为0(kn),一般k<2。所以该算法高效。
2、以下的代码时借助STL中的vector,用临界表来存储图的。
3、如果要输出一条最短路径对应的路线,我们可以用source[]表来记录。例如source[a]=b,
表示a的前驱为b。这样在执行完SPFA算法后,就会得到一张source表。然后从end向前一直,
找到start为止。就可产生一条路径了。当然,以上所说的只是比较简单的。比如要求在有多条
路径时打印经过节点最少的、字典序顺序小的。。。
4、SPFA算法不仅可以判断有向图、无向图任意两点之间是否有路径可达,还可以给出实际值。
5、一个关于SPFA算法的PPT,内容不错,免积分下载:SPFA算法简介
代码:
#include<iostream>#include<vector>#include<queue>#include<stack> #include<cstring>using namespace std;const int maxn=1001;const int INF=0x7fffffff;struct edge //边 { int to; int cost;}; vector<edge> myV[maxn]; //利用临界表存储图 int numNode,numEdge; //顶点数、边 int minPath[maxn]; //最短路int source[maxn]; //source[a]=b,说明a的前驱为b int start,end; //起点、终点 bool inQ[maxn]; //是否入队 void inputItial(){ int i,from,to,cost; for(i=0;i<maxn;i++) //清空再使用 { myV[i].clear(); } for(i=0;i<numEdge;i++) //建图 ,无向图 { scanf("%d%d%d",&from,&to,&cost); edge e; e.cost=cost; e.to=to; myV[from].push_back(e); e.to=from; myV[to].push_back(e); }}void output(int start,int end) //输出 { if(minPath[end]==INF) { printf("No Such Path Exist!\n\n"); } else if(start==end) { printf("From %d to %d :\n",start,end); printf("Path: %d\n",start); printf("Total cost : 0\n\n"); } else { printf("From %d to %d :\n",start,end); printf("Path: %d",start); int tmp=end; stack<int> s; s.push(tmp); while(source[tmp]!=start) { tmp=source[tmp]; s.push(tmp); } while(!s.empty()) { printf("-->%d",s.top()); s.pop(); } printf("\n"); printf("Total cost : %d\n\n",minPath[end]); } } void SPFA(int start,int end) //最短路径快速算法 Shortest Path Faster Algorithm{ memset(inQ,false,sizeof(inQ)); inQ[start]=true; for(int j=0;j<maxn;j++) minPath[j]=INF; minPath[start]=0; queue<int> myQ; myQ.push(start); int now,to,cost; while(!myQ.empty()) { now=myQ.front(); myQ.pop(); for(int k=0;k<myV[now].size();k++) { to=myV[now][k].to; cost=myV[now][k].cost+minPath[now]; if(minPath[to]>cost) { source[to]=now; //记录下to的来源为now minPath[to]=cost; if(!inQ[to]) { inQ[to]=true; myQ.push(to); } } } inQ[now]=false; } output(start,end); } int main(){ while(scanf("%d%d",&numNode,&numEdge)==2,numNode || numEdge) { inputItial(); while(scanf("%d%d",&start,&end)==2,start!=-1 && end!=-1) { SPFA(start,end); } } system("pause"); return 0;}
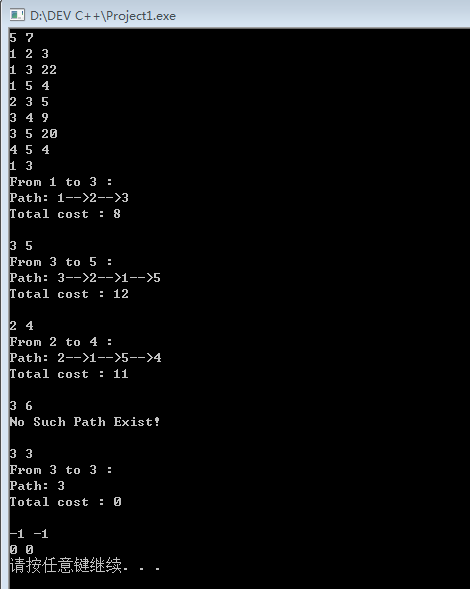
简单的小测试: