双目测距的几何原理
双目测距的几何原理
梁登 转载请注明http://blog.csdn.net/ldily110/
序言
做双目测距有一段时间了，这期间，我先后完成了基于matlab computer vision toolbox 和 opencv的双目测距，虽然谈不上有什么造诣，但是在高度的压力下，还是解决了很多问题，取得了一些成果。刚才收到jackjackhappy 网友的信件，说最近正在做双目测距方面的研究，但是找不到实现双目测距的方法，就是计算原理，已经做完摄像机标定和图像采集，接下来不知道怎样计算点的空间坐标。我想了一下，其实双目测距的方法网上有很多的资料，比如我手头的一本《学习opencv》书籍里第452页就有原理的阐释。但是我也可以理解这位网友的情况，对于很多已经工作的人，慢慢地去熟悉一个领域是一件很奢侈的事情，时间太仓促，进度的安排逼迫我们必须很短时间内站在一个领域的全局，理清整个流程，快速实现开发。有鉴于此，我将手头的一些资料整理一下，为自己理清思路，也给一些可能需要的人一些微小的帮助。以下内容了无新意，我仅仅是对现有资料做一些整理。
很多初学者对此很奇怪，觉得，咦怎么两张照片就莫名其妙的能计算出三维坐标呢？不可理解。其实，双目测距的背后隐含了两个前提
相机事先已经做好标定 （前提1）
两个相机的相对位置关系在拍摄照片时同他们在做标定时相一致 （前提2）
没有这两个前提，谈不上双目测距。可见，相机标定的问题是计算机视觉的基本问题，标定的精度直接决定了双目测距的准确性，甚至，标定误差大的时候，双目测距无法进行。
双目测距的几何模型是这样的，通常我们采用两个平行相机来拍摄图片，这样可以达到最佳的效果。
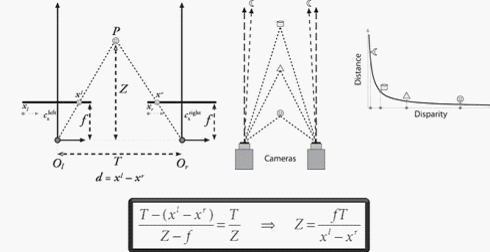
图 1
图1 是一张广为流传的图，阐释了双目测距的几何原理。如最左边的图所示，双目测距主要是利用了目标点在左右两幅视图上成像的横向坐标直接存在的差异（即视差
）与目标点到成像平面的距离Z存在着反比例的关系：在OpenCV中，f的量纲是像素点，T的量纲由定标板棋盘格的实际尺寸和用户输入值确定，一般是以毫米为单位（当然为了精度提高也可以设置为0.1毫米量级），d=xl-xr的量纲也是像素点。因此分子分母约去，Z的量纲与T相同。 ”。事实上，对于图1下部分的方框，能一下子看懂也不容易。
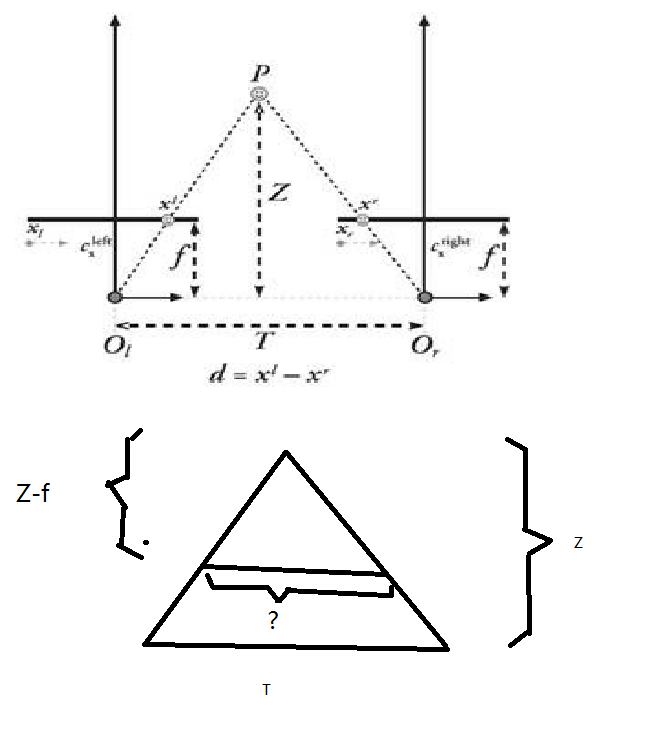
图 2
请注意，图2揭示了图1中，P处的深度Z的计算公式的原理，说白了，就是利用初中时就学过的相似三角形。只要表示出“？”部分代表的长度，就可以列出一个对应边成比例的关系式。
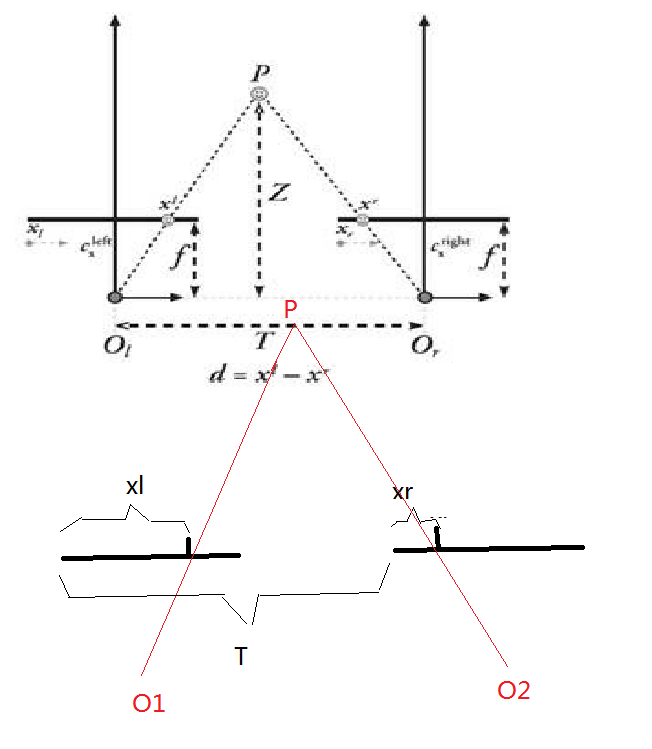
图 3 中画出了3条线段的长度，注意到 T+xr-xl 刚好就是两条小竖线之间的距离，也就是图2中“？”表示的部分。
至此，讲清楚了图1所述深度计算公式，以及各变量的含义。注意到，在图示中。xl,和 xr分别表示P点在左右相机的像平面的投影点（或者说成像点）到成像面最左侧（这里的左只是为了描述图片的方便，不要死扣）的物理距离，也就是已经以米 毫米等为单位，但是实际情况是，我们通过照片的标定，得到的焦距f只是以像素的尺寸为单位的，不是以物理长度如毫米为单位的，所以，在实际计算中，xl,和 xr还是用像素位置标示，也就是一个物体点在左右照片中对应的像素位置。
另外，注意到深度计算公式中有xl-xr做分母，这个在双目测距的理论中，称为视差(disparity)。直观地看，就是视差越大，说明对应点的深度越深，这和生活常识是相通的。隔相机越远的物体，在照片中的像素位置必然越接近。 在如下公式中，描述了两外两个维度的坐标计算方法。
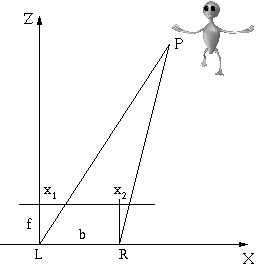
The Z-axis is the optical axis (the direction the cameras are pointing). b is the distance between cameras, while f is still the focal length. The equations of stereo triangulation (because it looks like a triangle) are:
Z_actual = (b * focal_length) / (x_camL - x_camR)
