SFFT比FFT更快的傅里叶变更

SFFT比FFT更快的傅里叶变化

最近MIT发布了一种新的FFT快速算法，SFFT，比原来的FFT要快10~100倍，这将引起相关的软件和硬件领域发生质的飞跃。

相关的介绍如下：

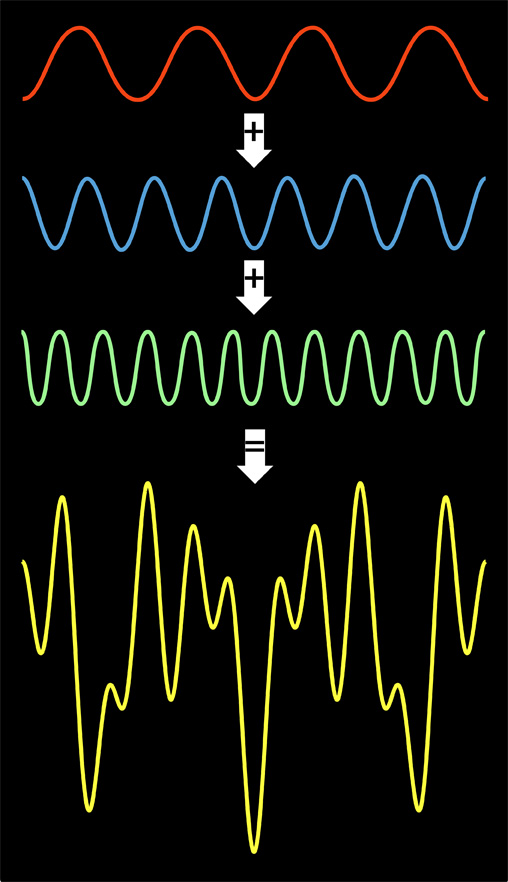
Sparse Fast Fourier Transform :The discrete Fourier transform (DFT) is one of the most important and widely used computational tasks. Its applications are broad and include signal processing, communications, and audio/image/video compression. Hence, fast algorithms for DFT are highly valuable. Currently, the fastest such algorithm is the Fast Fourier Transform (FFT), which computes the DFT of an n-dimensional signal inO(nlogn) time. The existence of DFT algorithms faster than FFT is one of the central questions in the theory of algorithms. 

A general algorithm for computing the exact DFT must take time at least proportional to its output size n. In many applications, however, most of the Fourier coefficients of a signal are small or equal to zero, i.e., the output of the DFT is sparse. This is the case for video signals, where a typical 8x8 block in a video frame has on average 7 non-negligible frequency coefficients (i.e., 89% of the coefficients are negligible). For sparse signals, the Ω(n)lower bound for the complexity of DFT no longer applies. If a signal has a small number k of non-zero Fourier coefficients the output of the Fourier transform can be represented succinctly using only k coefficients. Hence, for such signals, we can find DFT algorithms whose runtime is sublinear in the signal size, n. 

We present here several new results for sparse Fourier transform:

- An O(k log n)-time algorithm for the exactly k-sparse case.

- An O(k log n log(n/k))-time algorithm for the general case.

- An Ω(k log(n/k) loglog n) lower bound for sample complexity.

Both algorithms improve over FFT, for any k = o(n). Moreover, if one assume that FFT is optimal, the algorithm for the exactly k-sparse case is optimal. Under the same assumption, the result for the general case is at most one loglog n factor away from the optimal runtime for the case of 搇arge? sparsity k = n/log n.

Theory:

AlgorithmComplexity          Sparsity Range (k)sFFT 1.0 (Non-Iterative Alghorithm)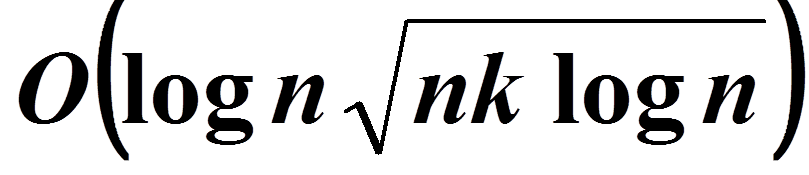 
::




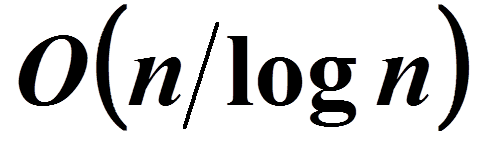sFFT 2.0 (sFFT 1.0 + Heuristic)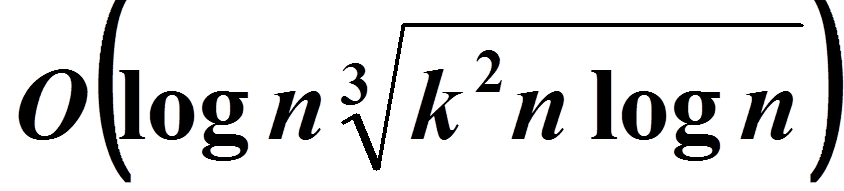 
::




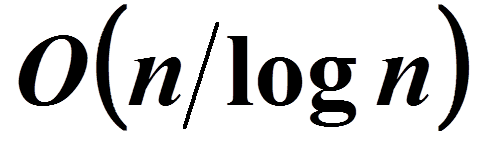sFFT 3.0 (Exact k Sparse Algorithm) 

::






sFFT 4.0 (General k Sparse Algorithm) 

:: 






Lower Bound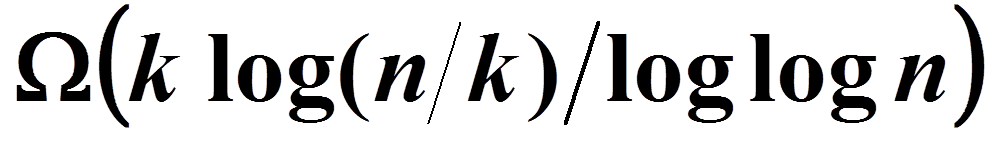 
::

Evaluation :
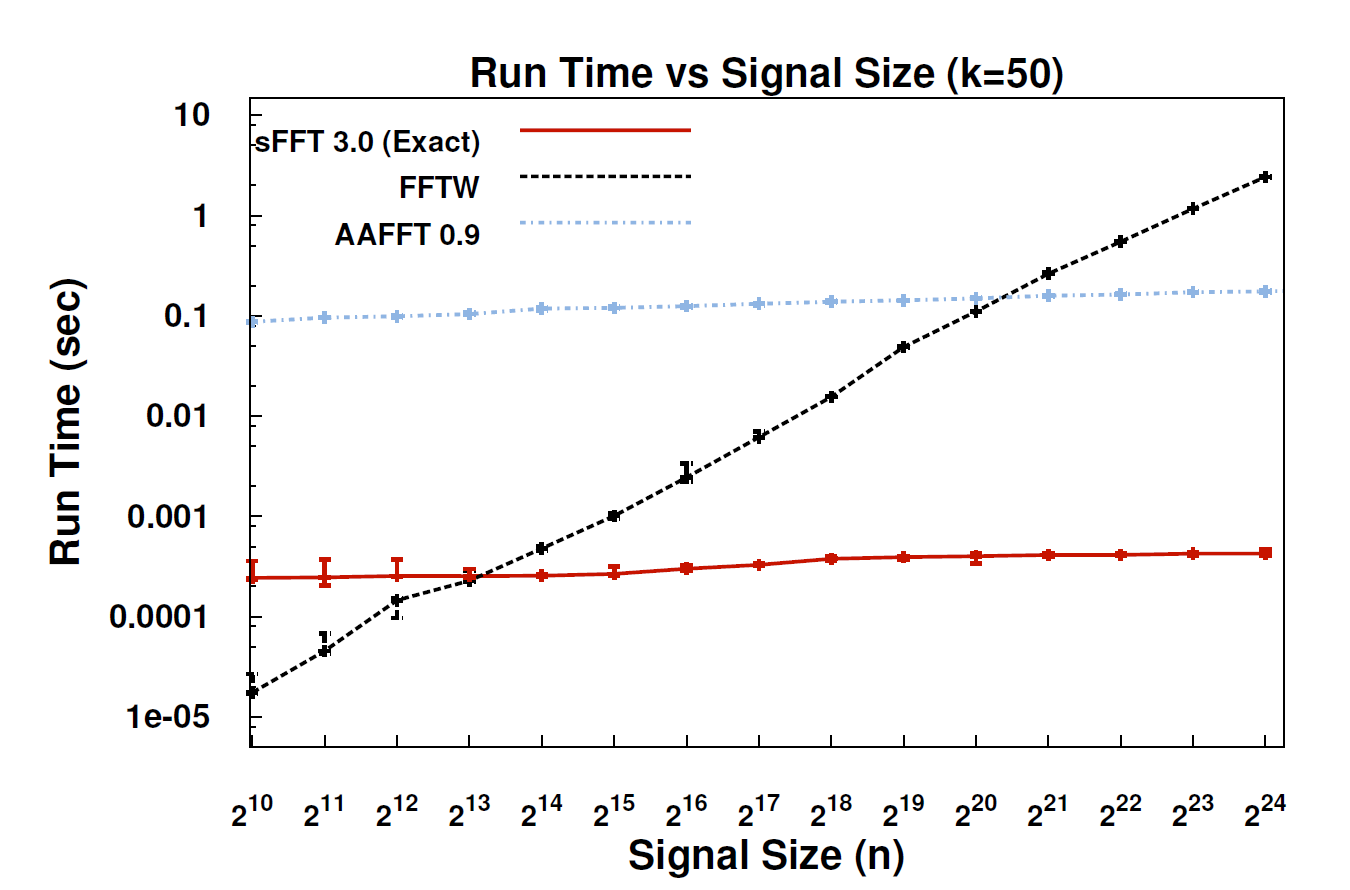
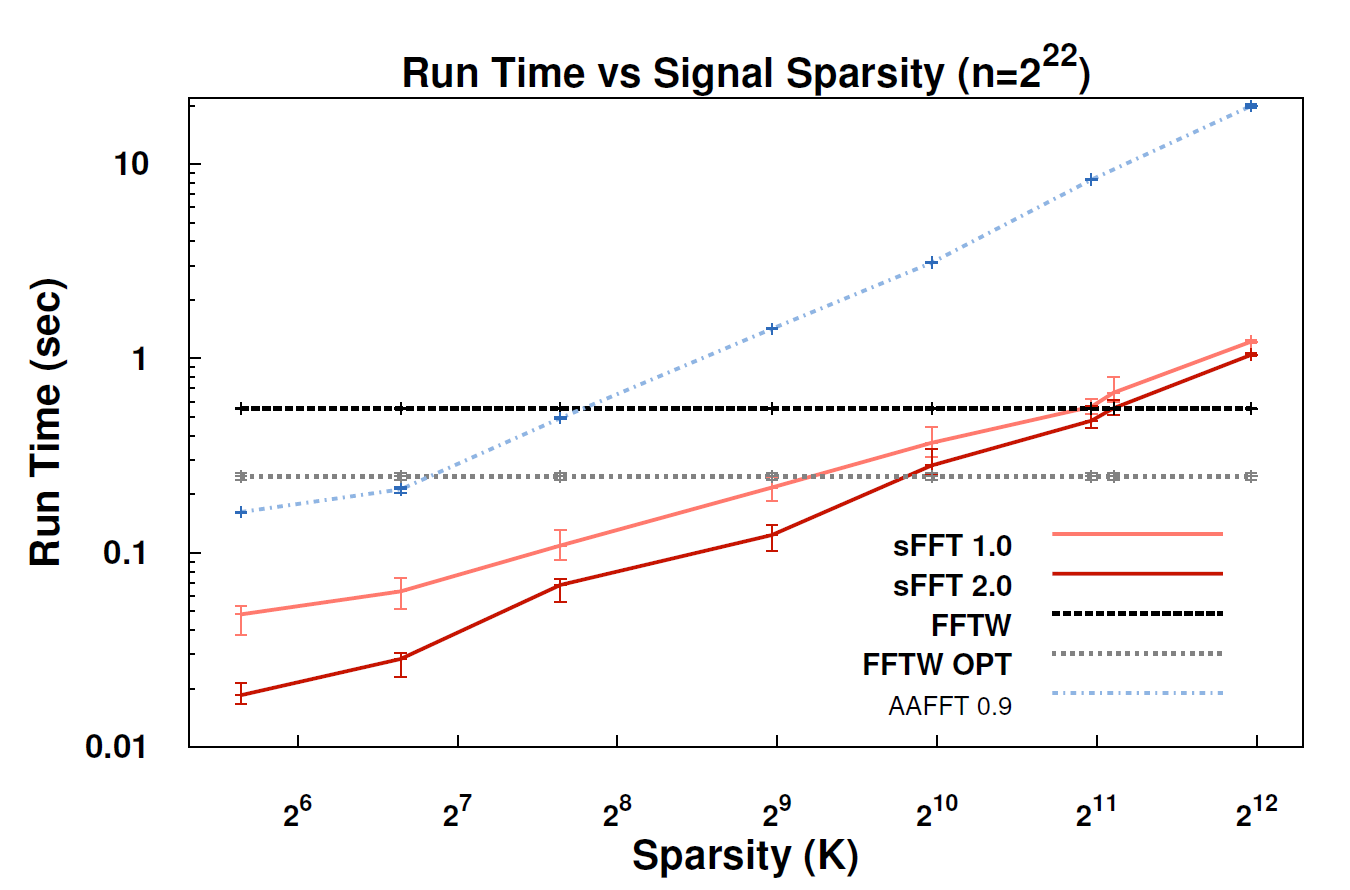
We compare our implementation of SFFT to FFTW (a very efficient implementation of the FFT algorithm) and to AAFFT (a recent algorithm that exploits sparsity to perform a faster fourier transform).

On the graphs to the left, we fix the sparsity of the signal (the number of non-zero frequencies K) and we vary the signal size N. On the graphs to the right, we fix the signal size N and vary the sparsity of the signal. 

The graphs on the top compare SFFT 3.0 (exact k sparse algorithm) with FFTW and AAFFT. The graphs below compare SFFT 1.0 and 2.0 to FFTW and AAFFT. You can click on each graph to enlarge. For a detailed comparison please refer to the papers in the Publicationssection. 

  


 

参考：

http://groups.csail.mit.edu/netmit/sFFT/code.html 

http://groups.csail.mit.edu/netmit/sFFT/index.html

http://groups.csail.mit.edu/netmit/sFFT/soda_paper.pdf