1.集合与简易逻辑


2.函数

3.数列

4.三角函数
(1)三角函数的图象和性质

(2)反三角函数与最简三角方程
反正弦 |x|≤1,arcsinx∈[-,],sin(arcsinx)=x,
反余弦 |x|≤1,arccosx∈[0,π],cos(arccosx)=x.
反正切 x∈R,arctanx∈(-,),tan(arctanx)=x.
方程 sinx=a,|a|≤1,则 x=2kπ+arcsina,或x=2kπ+π-arcsina,(k∈Z)
方程 cosx=a,|a|≤1,则 x=2kπ±arccosx,(k∈Z)
方程 tanx=a,a∈R,则 x=kπ+arctana,(k∈Z)
(3)加法定理与解斜三角形

(4)斜三角形的边角关系与面积

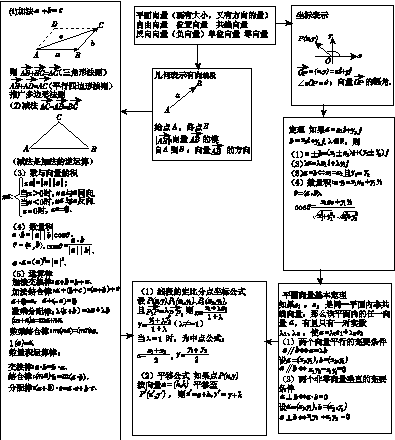
5.向量
6.直线和圆
|
基本公式 |
|
|
两点间 的距离 |
|AB|= |
|
线段的定比 分点公式 |
x=''y= |
|
线段的中点 坐标公式 |
x=''y= |
|
直线方程 |
|
|
斜截式 |
y=kx+b |
|
点斜式 |
y-y1=k(x-x1) |
|
两点式 |
(y-y1)(x2-x1)=(x-x1)(y2-y1) |
|
截距式 |
+=1 |
|
参数式 |
α为直线的倾角,t=P0P |
|
直线Ax+By+C=0(A2+B2≠0)的方向向量为(B,-A);法向量为(A,B) |
|
点P0(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离:
d=
两直线的交角:
l1到l2所成的角φ(l1、l2的斜率分别为k1、k2),tanφ=
l1到l2的夹角(不大于直角)φ0,tanφ0=